Question

In $\Delta ABC$and $\Delta DEF$, $AB=DE$, $AB\mid \mid DE$, $BC=EF$ and $BC\mid \mid EF$. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that
(i) quadrilateral ABED is a parallelogram

(ii) quadrilateral BEFC is a parallelogram

(iii) AD || CF and AD = CF

(iv) quadrilateral ACFD is a parallelogram

(v) AC = DF

(vi) ∆ ABC ≅ ∆ DEF.

Explanation

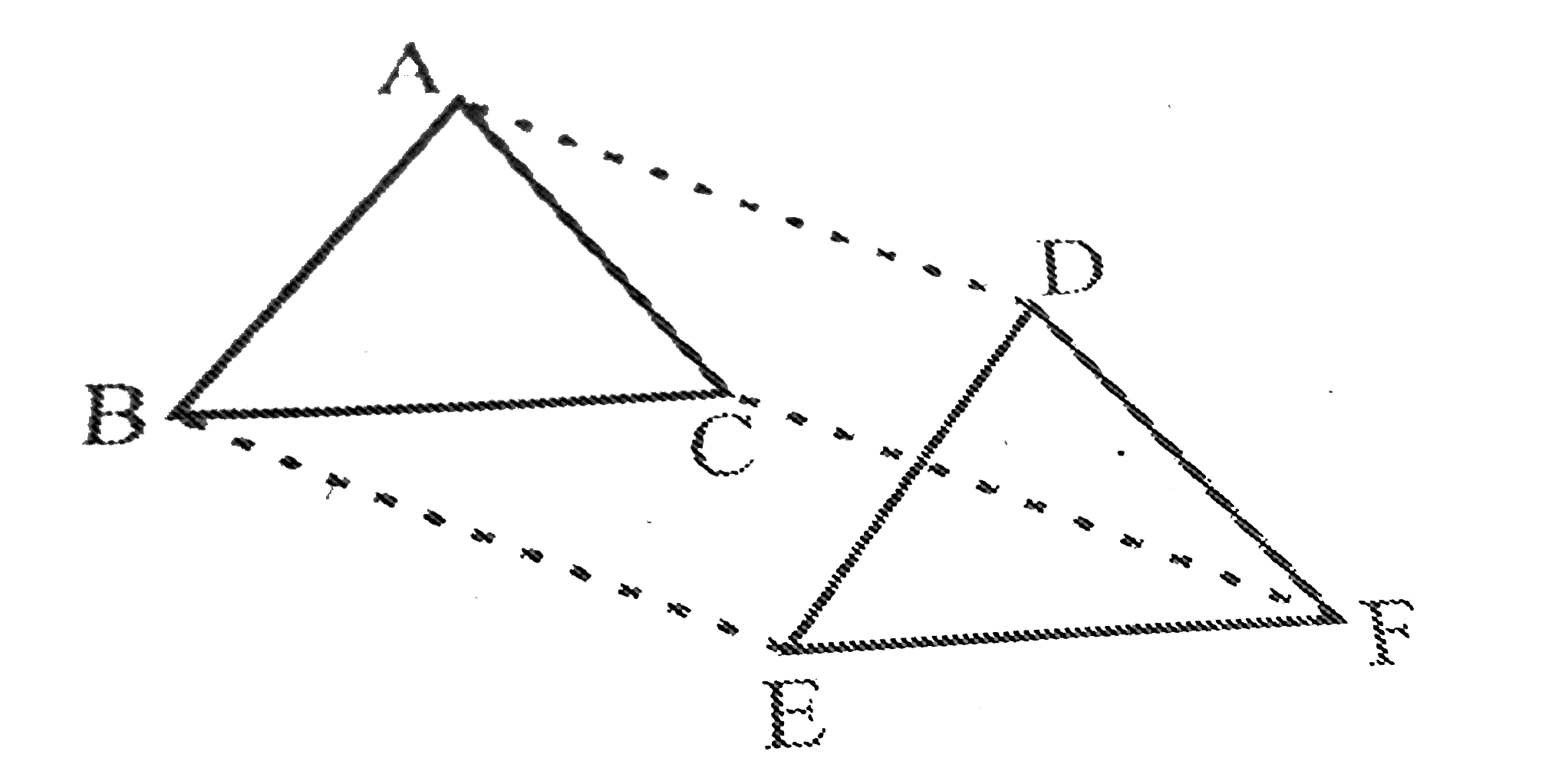
(i) Given, AB = DE and AB ||DE


If one pair of opposite sides of a quadrilateral are equal and parallel to each other,
then it is a parallelogram.

Thus, quadrilateral ABED is a parallelogram.


(ii)Again, BC = EF and BC || EF

Therefore, quadrilateral BEFC is a parallelogram using the concept discussed in (i).


(iii) As ABED and BEFC are parallelograms,

So,AD = BE and AD || BE
and ,BE = CF and BE || CF
(Opposite sides of a parallelogram are equal and parallel)

Therefore, AD = BE = CF and AD || BE || CF


(iv) As we observed that AD and CF are equal
and parallel to each other, therefore, it is a parallelogram.


(v) As ACFD is a parallelogram,
therefore, the pair of opposite sides will be equal and parallel to each other

∴ AC || DF and AC = DF


(vi) ∆ABC and ∆DEF,

=>BC = EF

=>AB = DE

=>AC = DF (Since ACFD is a parallelogram)

∴ ∆ABC ≅ ∆DEF (By SSS congruence rule)