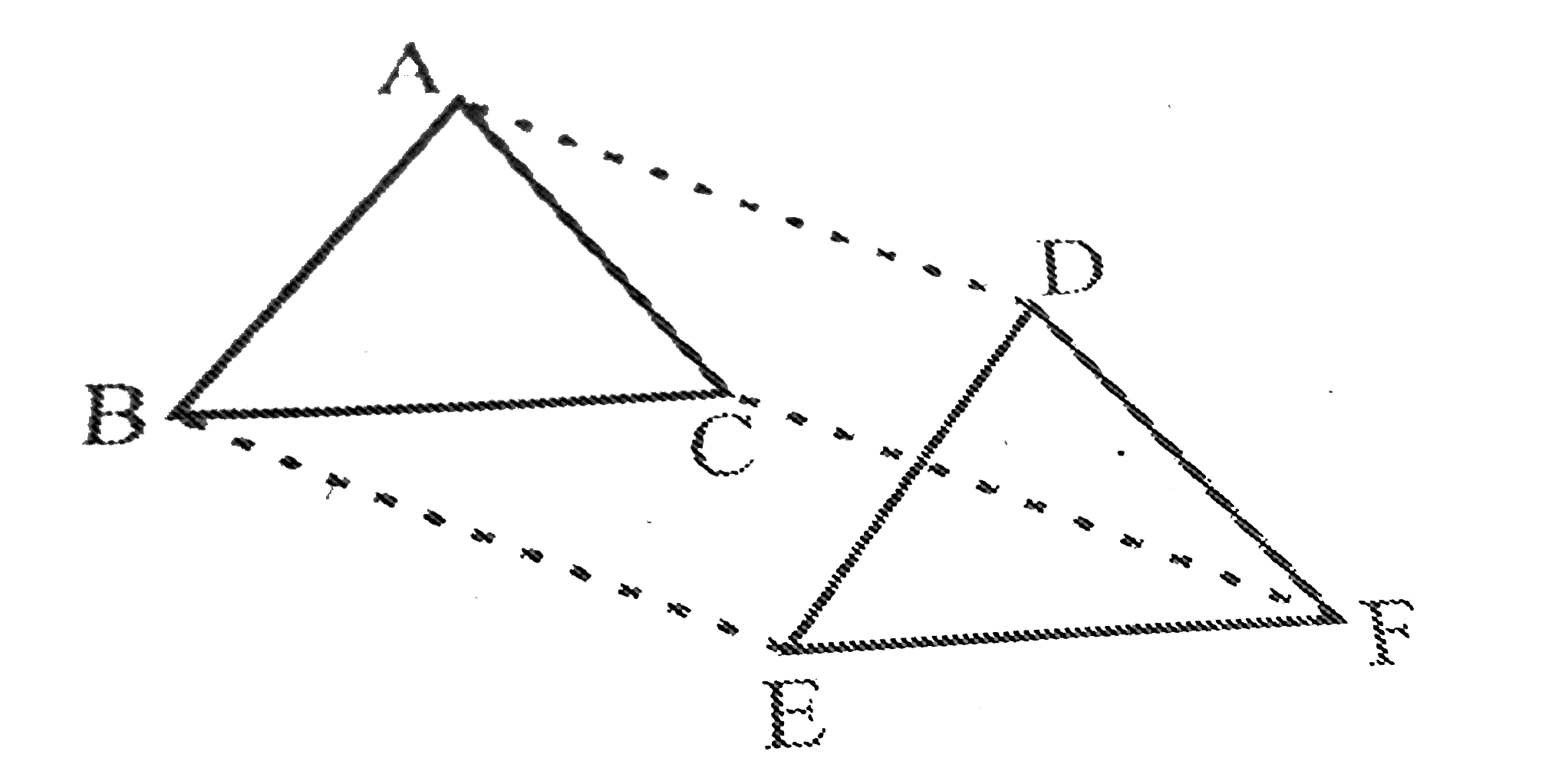
If ABC and DEF are two triangles such that AB,BC are respectively equal and parallel to DE,EF, then show that (i) quad ABED is a parallelogram (ii) quad BCFE is a paralellogram (iii) AC=DF (iv) ΔABC≅ΔDEF
Step by step video & image solution for If A B C and D E F are two triangles such that A B ,B C are respectively equal and parallel to D E ,E F , then show that (i) quad ABED is a parallelogram (ii) quad BCFE is a paralellogram (iii) AC=DF (iv) Delta ABC ~= Delta DEF by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF. Then show that
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BCFE is a parallelogram
(iii) AC=DF
(iv) ABC ≅ DEF
View SolutionIf ABC and DEF are similar triangles such that 2 AB=DE and BC=8cm , then EF=
View SolutionIn ΔABCand ΔDEF, AB = DE, AB ∣∣ DE, BC = EF and BC ∣∣ EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View SolutionIn triangle ABC, D and E are mid-points of sides AB and BC respectively. Also, F is a point in side AC so that DF is parallel to BC
(i) Prove that DBEF is a parallelogram.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View Solution
