In Figure, ABCD
is a trapezium in which AB∣∣CD
and AD=BC.
Show that :
(i) ∠A=∠B
(ii) ∠C=∠D
(iii) ABC≅BAD
(iv) diagonal AC=diagonalBD
(i) Given,AD=CE (Opposite sides of parallelogram AECD)
Also, AD=BC
Therefore, BC=CE
∠CEB=∠CBE (Angles opposite to equal sides in a triangle are equal)
⇒∠BAD+∠CEB=180°
⇒∠BAD+∠CBE=180°...(1)
[Since, ∠CEB = ∠CBE]
Also,
=> ∠ABC+∠CBE=180°...(2)
From (1) and (2), we see that
∠BAD=∠ABC
Thus, ∠A=∠B
(ii) Given,AB∣∣CD
⇒∠A+∠D=180°
⇒∠C+∠B=180°
∴ ∠A+∠D=∠C+∠B
However,∠A=∠B[From (i)]
Thus, ∠C=∠D
(iii) In ∆ABC and ∆BAD,
AB=BA (Common side)
BC=AD
∠B=∠A
∴ΔABC≅ΔBAD (SAS rule)
(iv) Since ΔABC≅ΔBAD,
∴AC=BD
Topper's Solved these Questions
- QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8.2
7 Videos
- PROBABILITYBOOK - NCERT ENGLISHCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES
10 Videos
- STATISTICSBOOK - NCERT ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 14.2
9 Videos
Similar Questions
In Figure, ABCD is a trapezium in which ABllCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D (iii) A B C~= B A D(iv)DiagonalA C=diagnol B D
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B .
View SolutionIn figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(△AOD)=ar(△BOC).
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: (i) ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
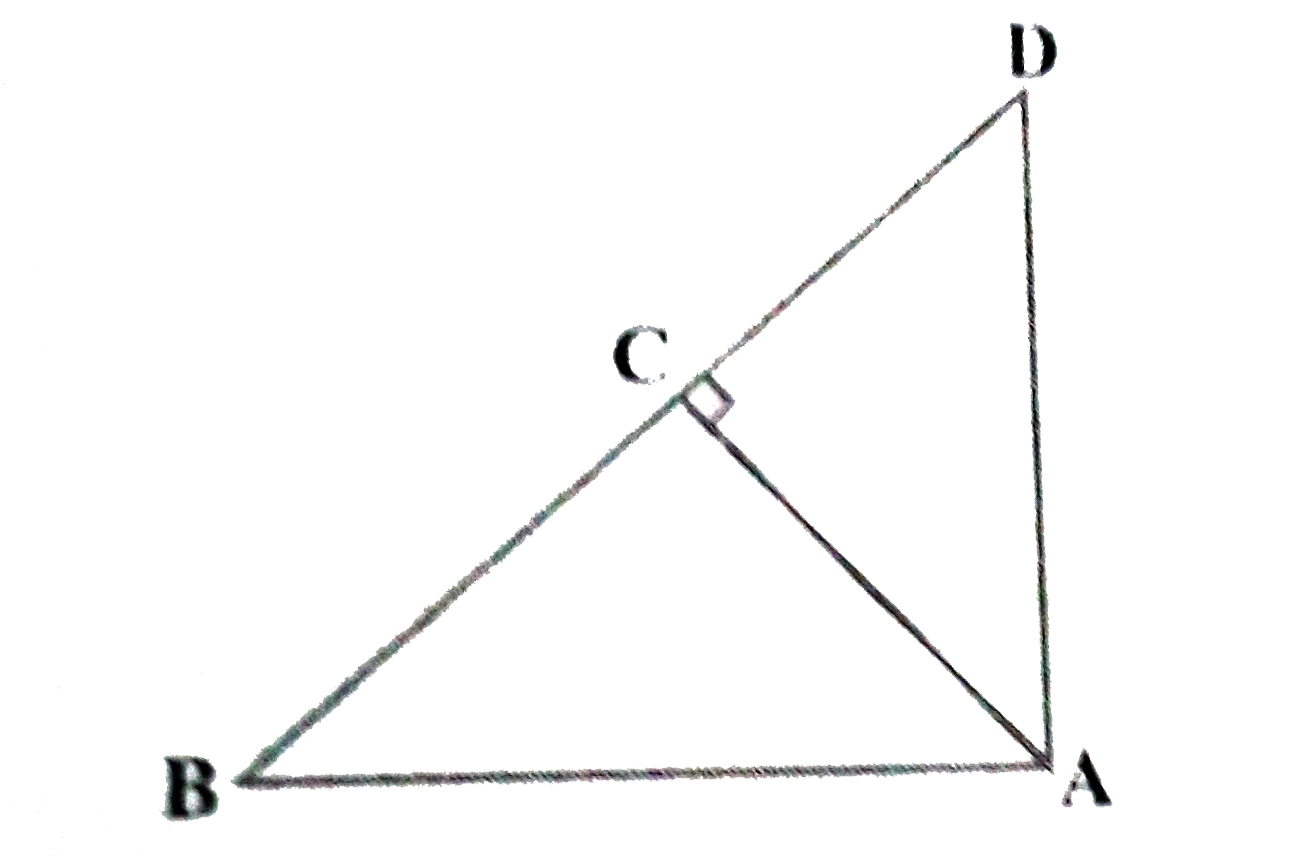
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn Figure, ABCD is a trapezium with AB∣∣DC . If △AED is similar to △BEC , prove that AD=BC .
View SolutionIn Figure, AD and BE are respectively perpendiculars to BC and AC . Show that: (i)△ADC~△BEC (ii)CA×CE=CB×CD (iii)△ABC~△DEC (iv)CD×AB=CA×DE
View SolutionIn Fig. 4.170, ABCD is a trapezium in which AB∥DC and AB=2 DC . Determine the ratio of the areas of AOB and COD . (FIGURE)
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAB=750and ∠DBC=600. Compute ∠CDB and ∠ADB
View Solution
