Question

D, E and F are respectively the mid-points of the sides BC, CA and AB of a$\Delta ABC$. Show that
(i) BDEF is a parallelogram.
(ii) $ar\left(DEF\right)=\frac{1}{4}ar\left(ABC\right)$
(iii) $ar\left(BDEF\right)=\frac{1}{2}ar\left(ABC\right)$

Explanation

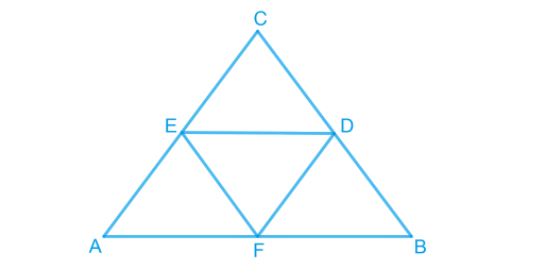
i) In ΔABC, D and E are the mid-points of side BC and AC respectively.


Therefore, the line joining points D and E will be parallel to line AB and also half of it as per the midpoint theorem.


The mid-point of AB is Fand E is the mid-point of AC


∴ `ED ║AB` and `ED = 1/2 AB`



Since `ED ║AB`.


Therefore, `ED ║FB` and `ED = FB` [F is the midpoint of AB]


Since one pair of the opposite side in quadrilateral BDEF is parallel and equal to each other, Therefore, `BDEF` is a parallelogram.


Similarly, we can prove, AEDF and CEFD are also parallelograms.


ii) Now, in parallelogram BDEF,


The diagonal DF of the parallelogram BDEF divides it into two triangles BDF and DEF of equal areas.




∴ `ar (ΔDEF) = ar (ΔBDF)`………..(i)


Similarly, DCEF is also parallelogram.


∴ `ar (ΔDEF) = ar (ΔDEC)`……….(ii)


Also,` AEDF` is a parallelogram.


∴ `ar (ΔDEF) = ar (ΔAFE)`……….(iii)


From equation (i), (ii) and (iii),


`ar (ΔDEF) = ar (ΔBDF) = ar (ΔDEC) = ar (ΔAFE)`……….(iv)


Now,


`ar (ΔABC) = ar (ΔDEF) + ar (ΔBDF) + ar (ΔDEC) + ar(ΔAFE)`……….(v)


`ar (ΔABC) = ar (ΔDEF) + ar (ΔDEF) + ar (ΔDEF) + ar (ΔDEF)` [Using (iv) & (v)]


`ar (ΔABC) = 4 × ar (ΔDEF)`



`ar (ΔDEF) = 1/4 ar (ΔABC)`



iii) `ar (║gm BDEF) = ar (ΔBDF) + ar (ΔDEF) = ar(ΔDEF) + ar (ΔDEF)`



`ar (║ gm BDEF) = 2 ar (ΔDEF)`



`ar (║ gm BDEF) = 2× 1/4 ar (ΔABC)`


`ar (║ gm BDEF) = 1/2 ar (ΔABC)`