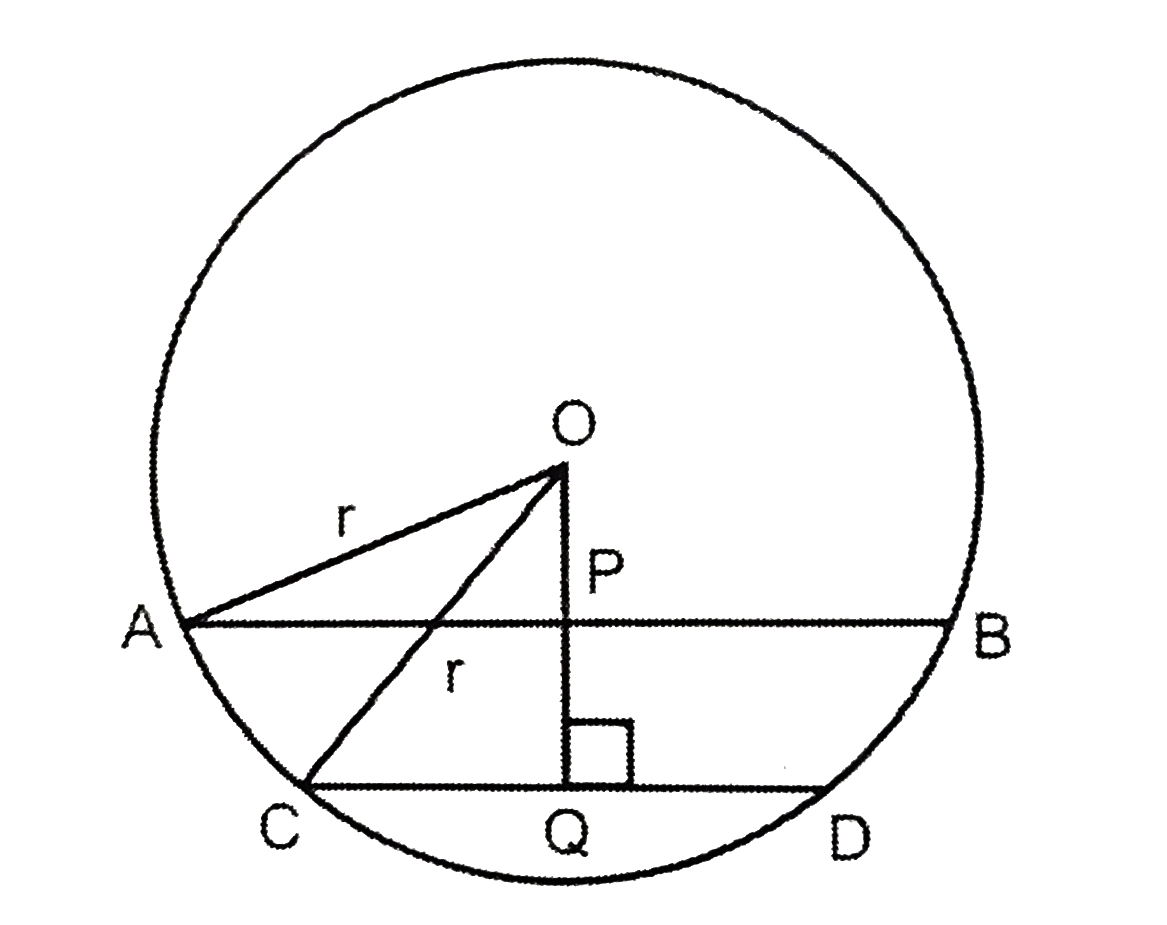
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.

Video Solution

Text Solution

Verified by Experts

$A B = 5 c m$ and $C D = 11 c m$
Distance between $A B$ and $C D$ is 3cm.
$O L$ and $O M$ are the perpendiculars on $C D$ and $A B$ respectively which bisect $C D$ and $A B$ .
Let $O L = x$ , then $O M = x + 3$
IN $△ O L D$
$O D^{2} = O L^{2} + L D^{2}$
$O D^{2} = x^{2} + {(5.5)}^{2}$
Similarly in $△ O M B$
$O B^{2} = {(x + 3)}^{2} + {(2.5)}^{2}$
But $O D$ and $O B$ are radii of a circle. Thus, $O D = O B$
${(x + 3)}^{2} + {(2.5)}^{2} = x^{2} + {(5.5)}^{2}$
$x^{2} + 6 x + 9 + 6.25 = x^{2} + 30.25$
$x = \frac{15}{6} = 2.5$
Now,
$O D^{2} = x^{2} + {(5.5)}^{2}$
$O D^{2} = {2.5}^{2} + 30.25$
$O D = \sqrt{36.5}$
$O D = \frac{\sqrt{146}}{2}$

|

Class 9 MATHS CIRCLES

Similar Questions

Knowledge Check

2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.
A15 cm
B14 cm
C13 cm
D12 cm

Recommended Questions

Home
Ask Doubt
Profile