A coin is tossed 1000 times with the following frequencies:Head : 455, Tail : 545Compute the probability for each event.
To solve the problem of finding the probability of getting heads and tails when a coin is tossed 1000 times, we can follow these steps:
Step 1: Identify the total number of tosses
The total number of times the coin is tossed is given as 1000.
Step 2: Determine the frequency of heads
The frequency of heads is given as 455.
Step 3: Calculate the probability of getting heads
The probability of an event is calculated using the formula:
Probability of Heads=Number of HeadsTotal Tosses
Substituting the values we have:
Probability of Heads=4551000
Step 4: Simplify the fraction
To simplify 4551000, we can divide both the numerator and the denominator by 5:
455÷51000÷5=91200
Step 5: Convert to decimal form
To convert 91200 to decimal form, we can perform the division:
91200=0.455
Step 6: Determine the frequency of tails
The frequency of tails is given as 545.
Step 7: Calculate the probability of getting tails
Using the same formula for probability:
Probability of Tails=Number of TailsTotal Tosses=5451000
Step 8: Simplify the fraction
To simplify 5451000, we can divide both the numerator and the denominator by 5:
545÷51000÷5=109200
Step 9: Convert to decimal form
To convert 109200 to decimal form, we perform the division:
109200=0.545
Final Results
- Probability of Heads: 91200 or 0.455
- Probability of Tails: 109200 or 0.545
---
The total number of times the coin is tossed is given as 1000.
The frequency of heads is given as 455.
The probability of an event is calculated using the formula:
To simplify 4551000, we can divide both the numerator and the denominator by 5:
To convert 91200 to decimal form, we can perform the division:
The frequency of tails is given as 545.
Using the same formula for probability:
To simplify 5451000, we can divide both the numerator and the denominator by 5:
To convert 109200 to decimal form, we perform the division:
- Probability of Heads: 91200 or 0.455
- Probability of Tails: 109200 or 0.545
Similar Questions
A coin is tossed 1000 times with the following frequencies: Head: 455, Tail : 545 Compute the probability for each event.
View SolutionA coin is tossed 1000 times with the following frequencies: Head : 455, Tail : 545 Compute the probability for each event.
View SolutionA coin is tossed 500 times with the following frequencies of two outcomes: Head: 240 times. tail: 260 times. Find the probability of occurrence of each of these events.
View SolutionA coin is tossed 500 times with the following frequencies of two outcomes:
head: 240 times, tail: 260 times.
Find the probability of occurrence of each of these events.
View SolutionTwo coins are tossed simultaneous 1000 times with the following frequencies of different outcomes: Two heads: 210 times One head: 550 times No head : 240 times Find the probability of occurrence of each of these events.
View SolutionTwo coins are tossed simultaneously 1000 times with the following frequencies of different outcomes:
Two heads: 210 times
One head: 550 times
No head: 240 times
Find the probability of occurrence of each of these events.
View SolutionA coin is tossed 100 times in which head is obtained 55 times. On tossing a coin at random find the probability of getting (i) a head (ii) a tail.
View SolutionTwo coins are tossed 1000 times and the outcomes are recorded as below
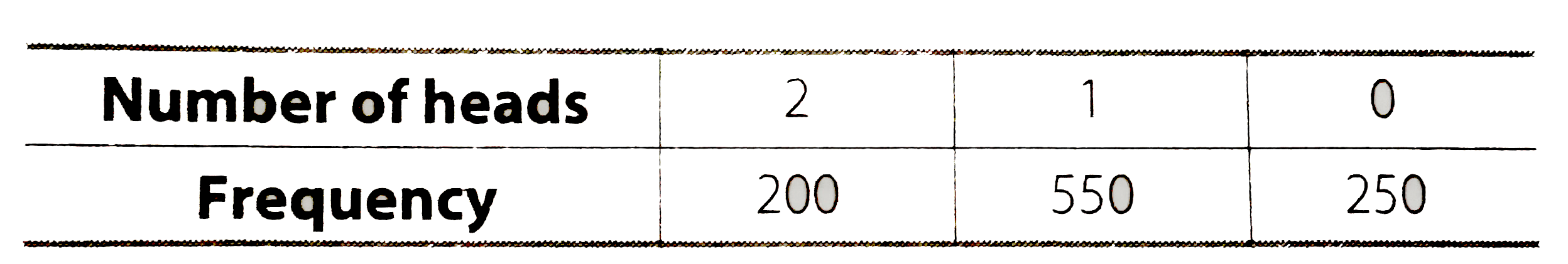
Based on this information, the probability for atmost one head is
View SolutionTwo coins are tossed simultaneous 500 times with the following frequencies of different outcomes.
Two tails = 110 times
One tail = 200 times
No tail = 190 times
Find the probability of occurrence of each events.
View SolutionThree coins are tossed simultaneously 100 times with the following frequencies of different outcomes:
Outcome:NoheadOneheadTwoheadsThreeHeadFrequency:14383612
If the three coins are simultaneously tossed again, compute the probability of:
(i)2 heads coming up. (ii) 3 heads coming up. (iii)at least one head coming up. (iv)getting more heads than tails. (v)getting more tails than heads
View Solution
