Two coins are tossed 1000 times and the outcomes are recorded as below
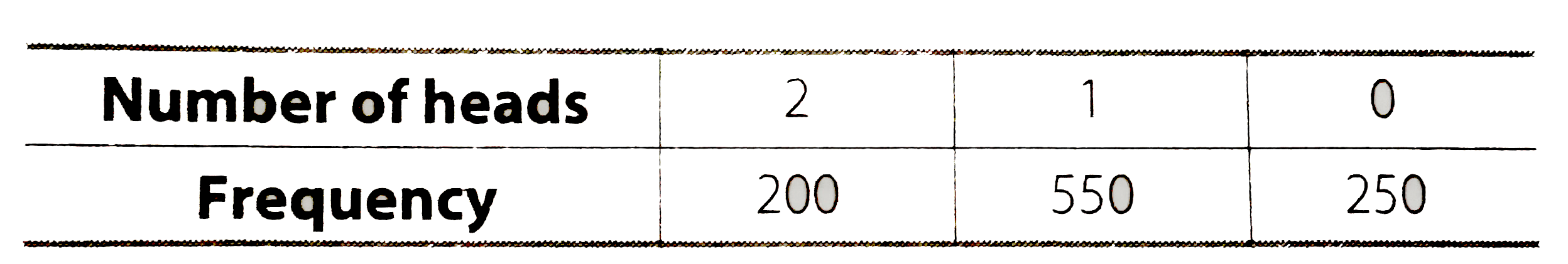
Based on this information, the probability for atmost one head is
15
14
45
34
The correct Answer is:C
The total number of coins tossed, n(S)=1000
Number of outcomes in which atmost one head, n( E)=550+250=800
∴ Probability for atmost one head =n(E)n(S)=8001000=45
Hence, the probability for atmost one head is 45.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWER TYPES QUESTIONS
10 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWER TYPE QUESTIONS
20 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - LONG ANSWER TYPE QUESTIONS
18 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
Similar Questions
Knowledge Check
A coin is tossed 4 times . The probability of getting atleast one head is
A116B18C78D1516
A coin is tossed two times. Find the probability of getting atmost one head.
View SolutionA coin is tossed three times and outcomes are recorded. How many possible outcomes are there?
View SolutionA coin is tossed eight times and outcomes are recorded. How many possible outcomes are there ?
View SolutionTwo coins are tossed simultaneously 500 times and the outcomes are noted as given below: Outcome: Two heads (HH) One head (HT or TH) No head (TT) Frequency: 105 275 120 If same pair of coins is tossed at random, find the probability of getting (i)Two heads (ii) One head (iii)No head
View SolutionTwo coins are tossed together. Find the probability of getting :
at most one head
View SolutionA coin is tossed 1000 times with the following frequencies: Head : 455, Tail : 545 Compute the probability for each event.
View SolutionTwo coins are tossed 1000 times and the outcomes are recorded as under :
∣∣∣Number of heads 2 1 0Frequency266 540 194∣∣∣
A coin is thrown at random. What is the probability of getting at most one head.
View Solution
