(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
To solve the problem step by step, we will analyze the patterns of matchsticks for squares and triangles.
Part (a): Matchstick Pattern of Squares
1. Identify the Pattern for Squares:
- For 1 square, we have 4 matchsticks.
- For 2 squares, we have 7 matchsticks.
- For 3 squares, we have 10 matchsticks.
- For 4 squares, we have 13 matchsticks.
2. Observe the Increment:
- From 1 square to 2 squares: 7 - 4 = 3 (increment of 3)
- From 2 squares to 3 squares: 10 - 7 = 3 (increment of 3)
- From 3 squares to 4 squares: 13 - 10 = 3 (increment of 3)
3. Establish a General Rule:
- The number of matchsticks increases by 3 for each additional square.
- Therefore, if we let n be the number of squares, the formula for the number of matchsticks M can be expressed as:
M=3n+1
4. Verification:
- For n=1: M=3(1)+1=4 (correct)
- For n=2: M=3(2)+1=7 (correct)
- For n=3: M=3(3)+1=10 (correct)
- For n=4: M=3(4)+1=13 (correct)
Part (b): Matchstick Pattern of Triangles
1. Identify the Pattern for Triangles:
- For 1 triangle, we have 3 matchsticks.
- For 2 triangles, we have 5 matchsticks.
- For 3 triangles, we have 7 matchsticks.
- For 4 triangles, we have 9 matchsticks.
2. Observe the Increment:
- From 1 triangle to 2 triangles: 5 - 3 = 2 (increment of 2)
- From 2 triangles to 3 triangles: 7 - 5 = 2 (increment of 2)
- From 3 triangles to 4 triangles: 9 - 7 = 2 (increment of 2)
3. Establish a General Rule:
- The number of matchsticks increases by 2 for each additional triangle.
- Therefore, if we let n be the number of triangles, the formula for the number of matchsticks M can be expressed as:
M=2n+1
4. Verification:
- For n=1: M=2(1)+1=3 (correct)
- For n=2: M=2(2)+1=5 (correct)
- For n=3: M=2(3)+1=7 (correct)
- For n=4: M=2(4)+1=9 (correct)
Summary of Rules:
- For squares: M=3n+1
- For triangles: M=2n+1
- For 1 square, we have 4 matchsticks.
- For 2 squares, we have 7 matchsticks.
- For 3 squares, we have 10 matchsticks.
- For 4 squares, we have 13 matchsticks.
- From 1 square to 2 squares: 7 - 4 = 3 (increment of 3)
- From 2 squares to 3 squares: 10 - 7 = 3 (increment of 3)
- From 3 squares to 4 squares: 13 - 10 = 3 (increment of 3)
- The number of matchsticks increases by 3 for each additional square.
- Therefore, if we let n be the number of squares, the formula for the number of matchsticks M can be expressed as:
M=3n+1
- For n=1: M=3(1)+1=4 (correct)
- For n=2: M=3(2)+1=7 (correct)
- For n=3: M=3(3)+1=10 (correct)
- For n=4: M=3(4)+1=13 (correct)
- For 1 triangle, we have 3 matchsticks.
- For 2 triangles, we have 5 matchsticks.
- For 3 triangles, we have 7 matchsticks.
- For 4 triangles, we have 9 matchsticks.
- From 1 triangle to 2 triangles: 5 - 3 = 2 (increment of 2)
- From 2 triangles to 3 triangles: 7 - 5 = 2 (increment of 2)
- From 3 triangles to 4 triangles: 9 - 7 = 2 (increment of 2)
- The number of matchsticks increases by 2 for each additional triangle.
- Therefore, if we let n be the number of triangles, the formula for the number of matchsticks M can be expressed as:
M=2n+1
- For n=1: M=2(1)+1=3 (correct)
- For n=2: M=2(2)+1=5 (correct)
- For n=3: M=2(3)+1=7 (correct)
- For n=4: M=2(4)+1=9 (correct)
- For squares: M=3n+1
- For triangles: M=2n+1
Topper's Solved these Questions
Similar Questions
Look at the following matchstick pattern of squares. The squares are not separate. Two neighboring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)
View SolutionFigs. Below gives a matchstick pattern of triangles. Find the general rule that gives the number of matchsticks in terms of the number of triangles.
View SolutionWrite the rule that gives the number of matchsticks required to make a pattern of letter M.
View SolutionFind the rule which gives the number of matchsticks required to make a pattern of n such shapes.
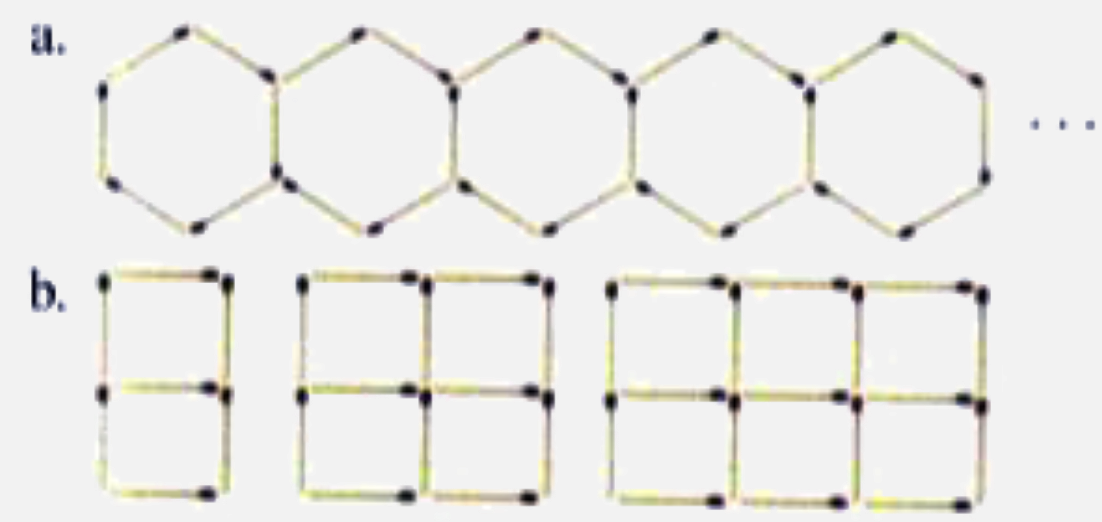
View SolutionWrite the rule that gives the number of matchsticks required to make the following pattern.

View SolutionFind a rule which gives the number of matchsticks required to make a pattern of the letter E as E
View SolutionFind the squares of the number127
View SolutionFind the rule that gives the number of matchsticks required to make the following pattern. Also, find the number of matchsticks required to make a pattern of 9 diamonds.

View SolutionFind a rule that gives the number of line segments required to make the following pattern of squares.
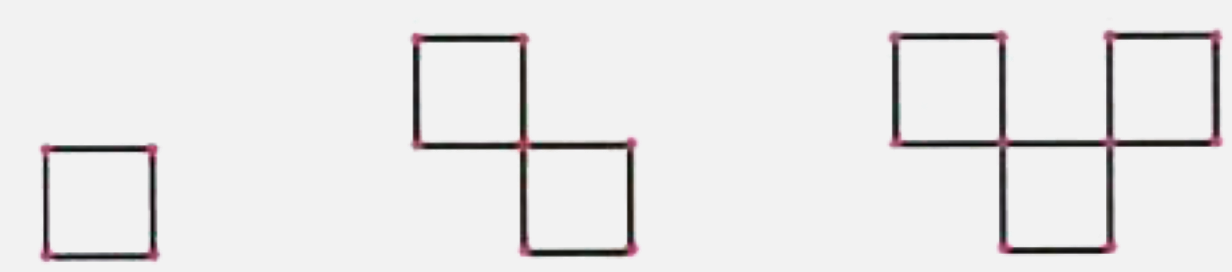
View SolutionFind the rule that gives the number of matchsticks required to build the following pattern. Also find the number of matchsticks required to make a pattern with 6 squares at the base.
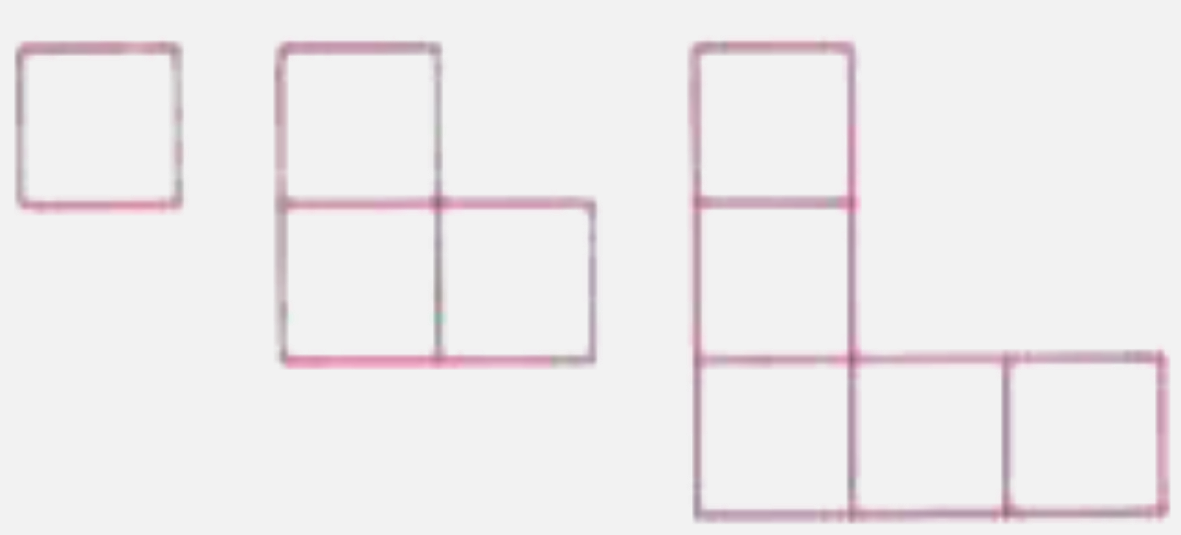
View Solution