Figs. Below gives a matchstick pattern of triangles. Find the general rule that gives the number of matchsticks in terms of the number of triangles.
To find the general rule that gives the number of matchsticks in terms of the number of triangles, we can analyze the pattern from the given figures step by step.
1. Identify the Number of Matchsticks for Each Figure:
- For Figure A (1 triangle):
- Matchsticks = 3
- For Figure B (2 triangles):
- Matchsticks = 5
- For Figure C (3 triangles):
- Matchsticks = 7
- For Figure D (4 triangles):
- Matchsticks = 9
2. Observe the Pattern:
- The number of matchsticks increases as the number of triangles increases.
- We can list the number of matchsticks corresponding to the number of triangles:
- 1 triangle → 3 matchsticks
- 2 triangles → 5 matchsticks
- 3 triangles → 7 matchsticks
- 4 triangles → 9 matchsticks
3. Find the Relationship:
- Notice that for each additional triangle, we add 2 matchsticks:
- From 1 to 2 triangles: 3 to 5 (add 2)
- From 2 to 3 triangles: 5 to 7 (add 2)
- From 3 to 4 triangles: 7 to 9 (add 2)
4. Formulate the General Rule:
- The pattern suggests that the number of matchsticks (M) can be expressed in terms of the number of triangles (X):
- The general rule can be written as:
M=2X+1
- Where M is the number of matchsticks and X is the number of triangles.
5. Verify the General Rule:
- For X = 1:
M=2(1)+1=3(Correct)
- For X = 2:
M=2(2)+1=5(Correct)
- For X = 3:
M=2(3)+1=7(Correct)
- For X = 4:
M=2(4)+1=9(Correct)
6. Using the General Rule for More Triangles:
- If we want to find the number of matchsticks for 5 triangles:
M=2(5)+1=10+1=11
- Therefore, for 5 triangles, we need 11 matchsticks.
Final Answer:
The general rule that gives the number of matchsticks in terms of the number of triangles is:
M=2X+1
Where M is the number of matchsticks and X is the number of triangles.
- For Figure A (1 triangle):
- Matchsticks = 3
- For Figure B (2 triangles):
- Matchsticks = 5
- For Figure C (3 triangles):
- Matchsticks = 7
- For Figure D (4 triangles):
- Matchsticks = 9
- The number of matchsticks increases as the number of triangles increases.
- We can list the number of matchsticks corresponding to the number of triangles:
- 1 triangle → 3 matchsticks
- 2 triangles → 5 matchsticks
- 3 triangles → 7 matchsticks
- 4 triangles → 9 matchsticks
- Notice that for each additional triangle, we add 2 matchsticks:
- From 1 to 2 triangles: 3 to 5 (add 2)
- From 2 to 3 triangles: 5 to 7 (add 2)
- From 3 to 4 triangles: 7 to 9 (add 2)
- The pattern suggests that the number of matchsticks (M) can be expressed in terms of the number of triangles (X):
- The general rule can be written as:
M=2X+1
- Where M is the number of matchsticks and X is the number of triangles.
- For X = 1:
M=2(1)+1=3(Correct)
- For X = 2:
M=2(2)+1=5(Correct)
- For X = 3:
M=2(3)+1=7(Correct)
- For X = 4:
M=2(4)+1=9(Correct)
- If we want to find the number of matchsticks for 5 triangles:
M=2(5)+1=10+1=11
- Therefore, for 5 triangles, we need 11 matchsticks.
The general rule that gives the number of matchsticks in terms of the number of triangles is:
M=2X+1
Where M is the number of matchsticks and X is the number of triangles.
Similar Questions
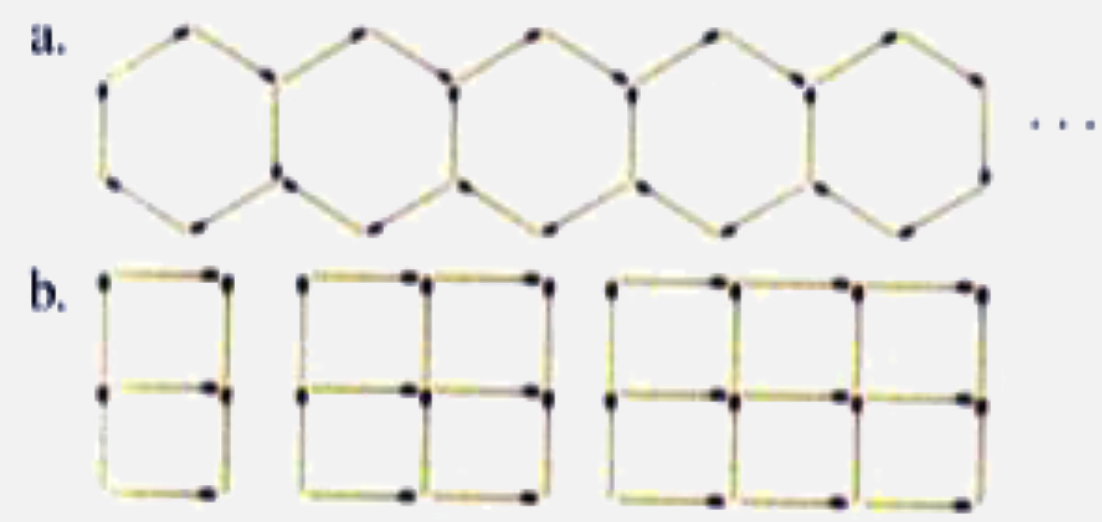
(a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.)(b) Fig 11.7 gives a matchstick pattern of triangles. As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles.
View SolutionLook at the following matchstick pattern of squares. The squares are not separate. Two neighboring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)
View SolutionWrite the rule that gives the number of matchsticks required to make a pattern of letter M.
View SolutionWrite the rule that gives the number of matchsticks required to make the following pattern.

View SolutionFind the rule which gives the number of matchsticks required to make a pattern of n such shapes.
View Solution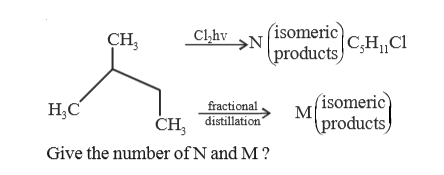
Give the number of N and M ?
View Solution
Give the number of N and M ?
View SolutionFind a rule which gives the number of matchsticks required to make a pattern of the letter E as E
View SolutionFind a rule that gives the number of line segments required to make the following pattern.

View SolutionFind a rule that gives the number of line segments required to make the following pattern of squares.

View Solution