If ΔDEF[≡~?]ΔBCA, write the part (s) of ΔBCA that correspond to (i) ∠E (ii) ∠¯¯¯¯¯¯EF (iii) <F (iv) ¯¯¯¯¯¯DF
To solve the problem, we need to identify the corresponding parts of triangle BCA based on the congruence with triangle DEF. Here's a step-by-step breakdown:
Step 1: Understand the Congruence
We know that triangle DEF is congruent to triangle BCA, which means that their corresponding angles and sides are equal.
Step 2: Identify Corresponding Vertices
From the congruence statement, we can establish the following correspondences between the vertices of the triangles:
- Vertex D corresponds to vertex B
- Vertex E corresponds to vertex C
- Vertex F corresponds to vertex A
Step 3: Find Corresponding Parts
Now, we will identify the corresponding parts of triangle BCA for each part of triangle DEF as follows:
(i) Angle E:
- Since angle E corresponds to vertex C, the part of triangle BCA that corresponds to angle E is angle C.
(ii) Side EF:
- Since E corresponds to C and F corresponds to A, the side EF corresponds to the side CA in triangle BCA. Therefore, the part of triangle BCA that corresponds to side EF is side CA.
(iii) Angle F:
- Since angle F corresponds to vertex A, the part of triangle BCA that corresponds to angle F is angle A.
(iv) Side DF:
- Since D corresponds to B and F corresponds to A, the side DF corresponds to the side BA in triangle BCA. Therefore, the part of triangle BCA that corresponds to side DF is side BA.
Summary of Correspondences:
- (i) Angle E corresponds to angle C.
- (ii) Side EF corresponds to side CA.
- (iii) Angle F corresponds to angle A.
- (iv) Side DF corresponds to side BA.
We know that triangle DEF is congruent to triangle BCA, which means that their corresponding angles and sides are equal.
From the congruence statement, we can establish the following correspondences between the vertices of the triangles:
- Vertex D corresponds to vertex B
- Vertex E corresponds to vertex C
- Vertex F corresponds to vertex A
Now, we will identify the corresponding parts of triangle BCA for each part of triangle DEF as follows:
- Since angle E corresponds to vertex C, the part of triangle BCA that corresponds to angle E is angle C.
- Since E corresponds to C and F corresponds to A, the side EF corresponds to the side CA in triangle BCA. Therefore, the part of triangle BCA that corresponds to side EF is side CA.
- Since angle F corresponds to vertex A, the part of triangle BCA that corresponds to angle F is angle A.
- Since D corresponds to B and F corresponds to A, the side DF corresponds to the side BA in triangle BCA. Therefore, the part of triangle BCA that corresponds to side DF is side BA.
- (i) Angle E corresponds to angle C.
- (ii) Side EF corresponds to side CA.
- (iii) Angle F corresponds to angle A.
- (iv) Side DF corresponds to side BA.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- COMPARING QUANTITIESBOOK - NCERT ENGLISHCHAPTER - COMPARING QUANTITIESEXERCISE - EXERCISE 8.2
10 Videos
- DATA HANDLINGBOOK - NCERT ENGLISHCHAPTER - DATA HANDLINGEXERCISE - EXERCISE 3.2
5 Videos
Similar Questions
ΔABCandΔPQR are congruent under the correspondence : ABC↣RQP write the parts of ΔABC that correspond to ? (i) ∠P (ii) ∠Q (iii) ¯¯¯¯¯Rp
View SolutionWrite short notes on :
(i) Free radicals (ii) Carbenes (iii) Nitrenes.
View SolutionWrite the names and structures of the monomers of the following polyers :
(i) Buna -S
(ii) Neoprene
(iii) Teflon
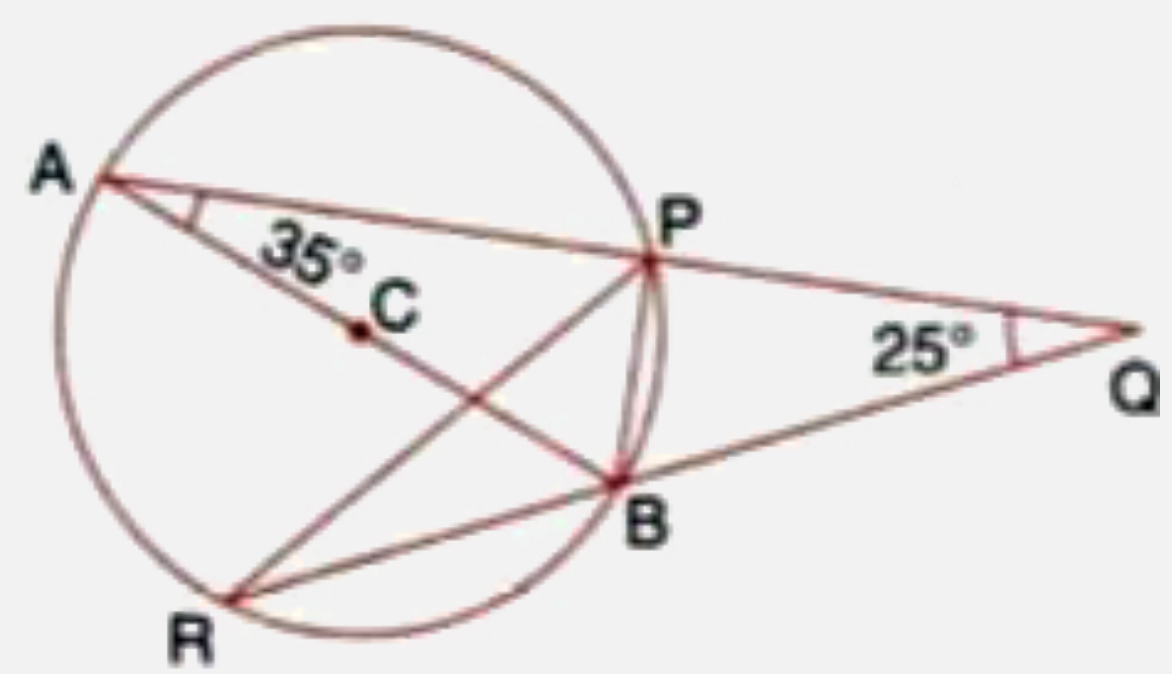
View SolutionAB is a diameter of the circle APBR at shown in the figure. APQ and RBQ are straight lines
Find :
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR.
View SolutionWrite the supplement of each of the following angles: (i) 540 (ii) 1320 (iii) 1380
View SolutionIn the adjoining figure, identify(i) the pairs of corresponding angles.(ii) the pairs of alternate interior angles.(iii) the pairs of interior angles on the sameside of the transversal.(iv) the vertically opposite angles.
View SolutionWrite the set of factors of :
(i) 88 (ii) 105 (iii) 96
View SolutionWrite the names and structures of the monomers of the following polymers :
(i) Buna-S
(ii) Neoprene
(iii) Nylon-6
View SolutionWrite the names and structures of the monomers of the folfowing polymers : (i) Terylene, (ii) Buna-S, (iii) Neoprene
View SolutionWrite the fraction representing the shaded parts: Figure (ii) Figure (iii) Figure (iv) Figure
View Solution
