DL and BM are the height on sides AB and AD respectively of parallelogram ABCD. If the area of the parallelogram is 1470 cm2,AB=35 cmandAD=49 cm find the BM and DL.
To solve the problem, we need to find the heights DL and BM of the parallelogram ABCD using the given area and the lengths of the sides AB and AD.
Step 1: Understand the Area Formula
The area A of a parallelogram can be calculated using the formula:
A=base×height
where the base can be any side of the parallelogram, and the height is the perpendicular distance from the opposite side to that base.
Step 2: Calculate DL
We will use side AB as the base to find height DL.
Given:
- Area A=1470cm2
- Length of AB=35cm
Using the area formula:
1470=AB×DL
Substituting the value of AB:
1470=35×DL
Now, we solve for DL:
DL=147035
Calculating DL:
DL=42cm
Step 3: Calculate BM
Next, we will use side AD as the base to find height BM.
Given:
- Length of AD=49cm
Using the area formula again:
1470=AD×BM
Substituting the value of AD:
1470=49×BM
Now, we solve for BM:
BM=147049
Calculating BM:
BM=30cm
Final Answers
- DL=42cm
- BM=30cm
The area A of a parallelogram can be calculated using the formula:
A=base×height
where the base can be any side of the parallelogram, and the height is the perpendicular distance from the opposite side to that base.
We will use side AB as the base to find height DL.
- Area A=1470cm2
- Length of AB=35cm
1470=AB×DL
Substituting the value of AB:
1470=35×DL
DL=147035
Calculating DL:
DL=42cm
Next, we will use side AD as the base to find height BM.
- Length of AD=49cm
1470=AD×BM
Substituting the value of AD:
1470=49×BM
BM=147049
Calculating BM:
BM=30cm
- DL=42cm
- BM=30cm
Topper's Solved these Questions
Similar Questions
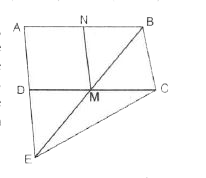
L and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View SolutionIn the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.
If the area of parallelogram ABCD is 48cm2,
(i) State the area of the triangle BEC.
(ii) name the parallelofram which is equal in area to the triangle BEC.
View Solution
Knowledge Check
The base of a parallelogram is one - third of it’s height, the area of this parallelogram is 147cm2 , find its height .
A=24 cm .B=21 cm .C=22 cm .D=23 cm .
Find the area of the parallelogram having :
base = 14.5 cm , height = 2.4 cm
View SolutionFind the height ‘x’ if the area of the parallelogram is 24cm2and the base is4 cm.
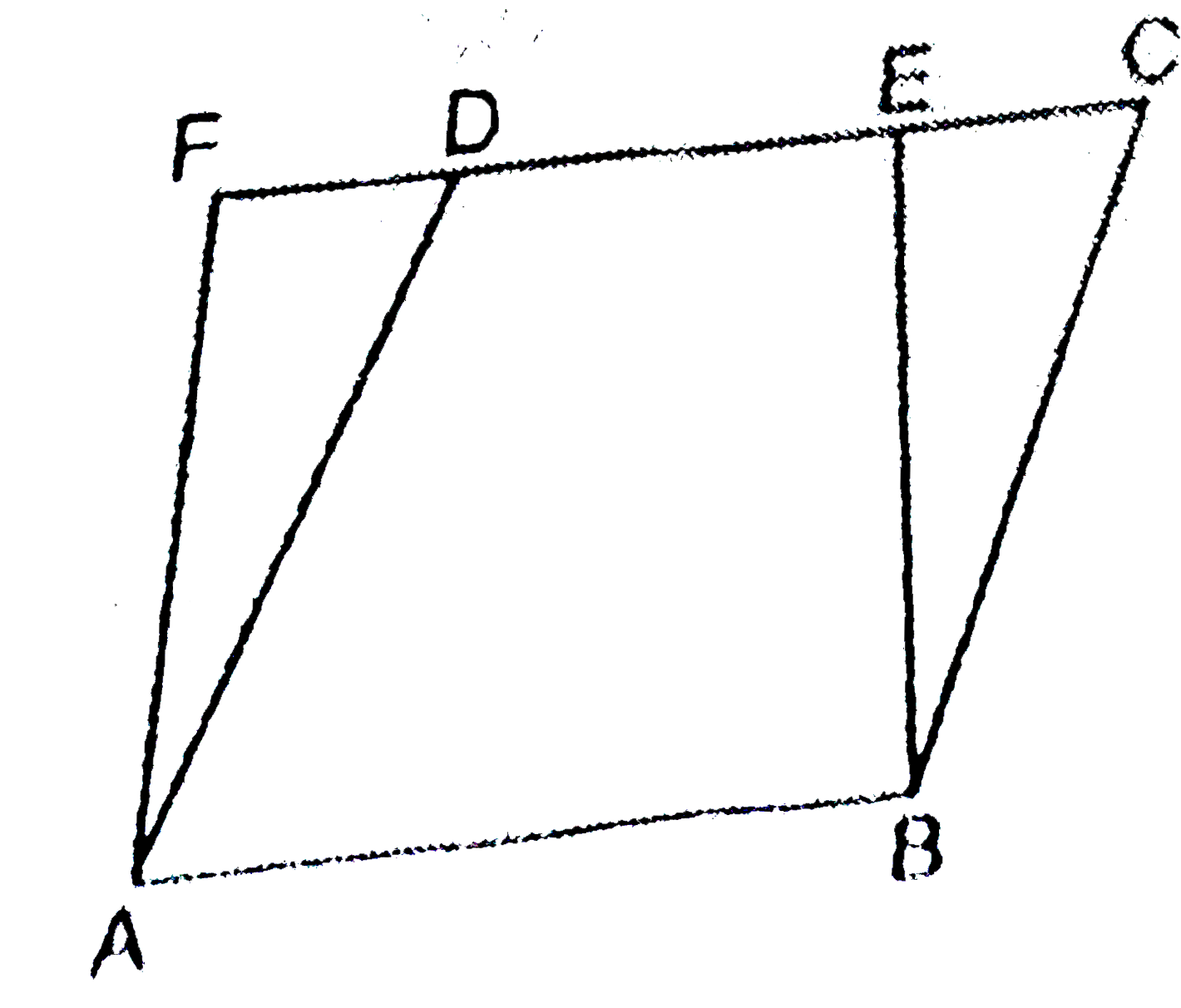
View SolutionIn the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
View SolutionThe height of a parallelogram is three-eighths of its base. If the area of the parallelogram is 96cm2 , find its height and base .
View SolutionFind the area of a parallelogram with base 5 cm and altitude 4.2 cm.
View SolutionThe base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View Solution
