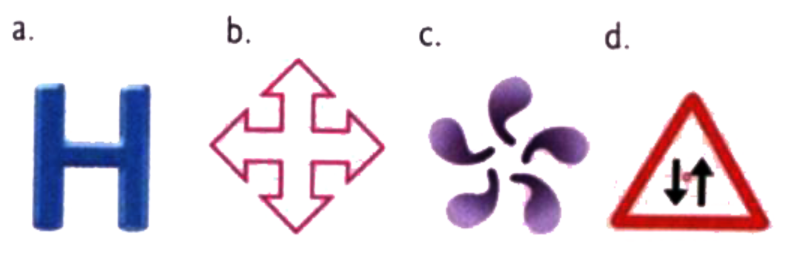
Which of the following figures have rotational symmetry of order more than 1:
To determine which of the given figures have rotational symmetry of order more than one, we need to analyze each figure based on the definition of rotational symmetry.
1. Understanding Rotational Symmetry:
- A figure has rotational symmetry if it can be rotated around its center and still look the same. The order of rotational symmetry is the number of times a figure matches itself during a full rotation (360 degrees).
2. Analyzing Figure A:
- If we rotate Figure A by 90 degrees, it looks the same. We can rotate it 4 times (90°, 180°, 270°, and 360°) and it will match itself each time.
- Conclusion: Figure A has rotational symmetry of order 4 (more than 1).
3. Analyzing Figure B:
- Figure B is an equilateral triangle. If we rotate it by 120 degrees, it matches itself. We can rotate it 3 times (120°, 240°, and 360°) and it will look the same.
- Conclusion: Figure B has rotational symmetry of order 3 (more than 1).
4. Analyzing Figure C:
- For Figure C, if we rotate it by 360 degrees, it looks the same, but it does not match itself at any angle less than 360 degrees.
- Conclusion: Figure C has rotational symmetry of order 1 (not more than 1).
5. Analyzing Figure D:
- Similar to Figure A, if we rotate Figure D by certain degrees (like 90 degrees), it matches itself multiple times.
- Conclusion: Figure D has rotational symmetry of order more than 1.
6. Analyzing Figure E:
- Figure E can also be rotated (like a star) and will match itself at certain angles.
- Conclusion: Figure E has rotational symmetry of order 3 (more than 1).
7. Analyzing Figure F:
- Figure F, like the others, can be rotated and will match itself multiple times.
- Conclusion: Figure F has rotational symmetry of order more than 1.
Final Summary:
- Figures with rotational symmetry of order more than 1: A, B, D, E, F.
- Figure with rotational symmetry of order 1: C.
- A figure has rotational symmetry if it can be rotated around its center and still look the same. The order of rotational symmetry is the number of times a figure matches itself during a full rotation (360 degrees).
- If we rotate Figure A by 90 degrees, it looks the same. We can rotate it 4 times (90°, 180°, 270°, and 360°) and it will match itself each time.
- Conclusion: Figure A has rotational symmetry of order 4 (more than 1).
- Figure B is an equilateral triangle. If we rotate it by 120 degrees, it matches itself. We can rotate it 3 times (120°, 240°, and 360°) and it will look the same.
- Conclusion: Figure B has rotational symmetry of order 3 (more than 1).
- For Figure C, if we rotate it by 360 degrees, it looks the same, but it does not match itself at any angle less than 360 degrees.
- Conclusion: Figure C has rotational symmetry of order 1 (not more than 1).
- Similar to Figure A, if we rotate Figure D by certain degrees (like 90 degrees), it matches itself multiple times.
- Conclusion: Figure D has rotational symmetry of order more than 1.
- Figure E can also be rotated (like a star) and will match itself at certain angles.
- Conclusion: Figure E has rotational symmetry of order 3 (more than 1).
- Figure F, like the others, can be rotated and will match itself multiple times.
- Conclusion: Figure F has rotational symmetry of order more than 1.
- Figures with rotational symmetry of order more than 1: A, B, D, E, F.
- Figure with rotational symmetry of order 1: C.
Topper's Solved these Questions
- SYMMETRYBook:NCERT ENGLISHChapter:SYMMETRYExercise:EXERCISE 14.1
Explore 9 Videos
- SIMPLE EQUATIONSBook:NCERT ENGLISHChapter:SIMPLE EQUATIONSExercise:EXERCISE 4.4
Explore 3 Videos
- THE TRIANGLE AND ITS PROPERTIESBook:NCERT ENGLISHChapter:THE TRIANGLE AND ITS PROPERTIESExercise:EXERCISE 6.2
Explore 2 Videos
Similar Questions
Knowledge Check
Which of the following figures has only one line of symmetry ?
AA rectangleBA parallelogramCAn isosceles trapeziumDA circleWhich of the following compounds have the plane of symmetry?
A B
B C
C D
D
If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
View SolutionName the quadrilaterals which have both line and rotational symmetry of order more than 1.
View SolutionWhich has no rotation of symmetry ?
View SolutionWhich of the given figures show line/reflection symmetry?
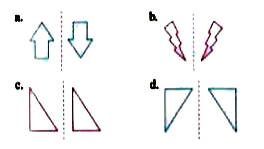 .
.
View SolutionWhich of the following is more elastic than air ?
View SolutionWhich of the following is more basic than aniline?
View Solution