The resistance R=VI, where V=(100±5.0)V and I=(10±0.2)A. Find the percentage error in R.
To find the percentage error in the resistance R given by the formula R=VI, where V=(100±5.0)V and I=(10±0.2)A, we can follow these steps:
Step 1: Identify the values and their uncertainties
- Voltage V=100V with an uncertainty ΔV=5V
- Current I=10A with an uncertainty ΔI=0.2A
Step 2: Write the formula for resistance
The resistance R is given by:
R=VI
Step 3: Calculate the percentage error in V and I
The percentage error in a quantity is given by:
Percentage Error=ΔXX×100
For Voltage V:
Percentage Error in V=ΔVV×100=5100×100=5%
For Current I:
Percentage Error in I=ΔII×100=0.210×100=2%
Step 4: Calculate the total percentage error in R
The total percentage error in R can be calculated using the formula for the propagation of errors in division:
Total Percentage Error in R=Percentage Error in V+Percentage Error in I
Total Percentage Error in R=5%+2%=7%
Final Result
Thus, the percentage error in the resistance R is:
Percentage Error in R=7%
---
- Voltage V=100V with an uncertainty ΔV=5V
- Current I=10A with an uncertainty ΔI=0.2A
The resistance R is given by:
R=VI
The percentage error in a quantity is given by:
Percentage Error=ΔXX×100
Percentage Error in V=ΔVV×100=5100×100=5%
Percentage Error in I=ΔII×100=0.210×100=2%
The total percentage error in R can be calculated using the formula for the propagation of errors in division:
Total Percentage Error in R=Percentage Error in V+Percentage Error in I
Total Percentage Error in R=5%+2%=7%
Thus, the percentage error in the resistance R is:
Percentage Error in R=7%
Topper's Solved these Questions
Similar Questions
The resistance R=V/i, where V=100±5VandI=10±0.2A. What is the total error in R?
View SolutionThe resistant R=V/I where V=100±0.5V and I=10±0.2A. The percentage error in V is 5% and in I is 2%. Find the total percentage error is R.
View SolutionIf voltage V=(100±5) V and current I=(10±0.2) A, the percentage error in resistance R is
View SolutionWhen the voltage and current in a conductor are measured as (100±4)Vand(5±0.2) A, then the percentage of error in the calculation of resistance is
View SolutionThe voltage and current in a conductor are measured as (50±2)Vand(5±0.2)A The percentage error in the calculation of resistance is
View SolutionThe resistance of metal is given by V=IR, The voltage in the resistance is V=(8±0.5)V and current in the resistance is I=(2±0.2)A, the value fo resistance with its percentage error is
View SolutionThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
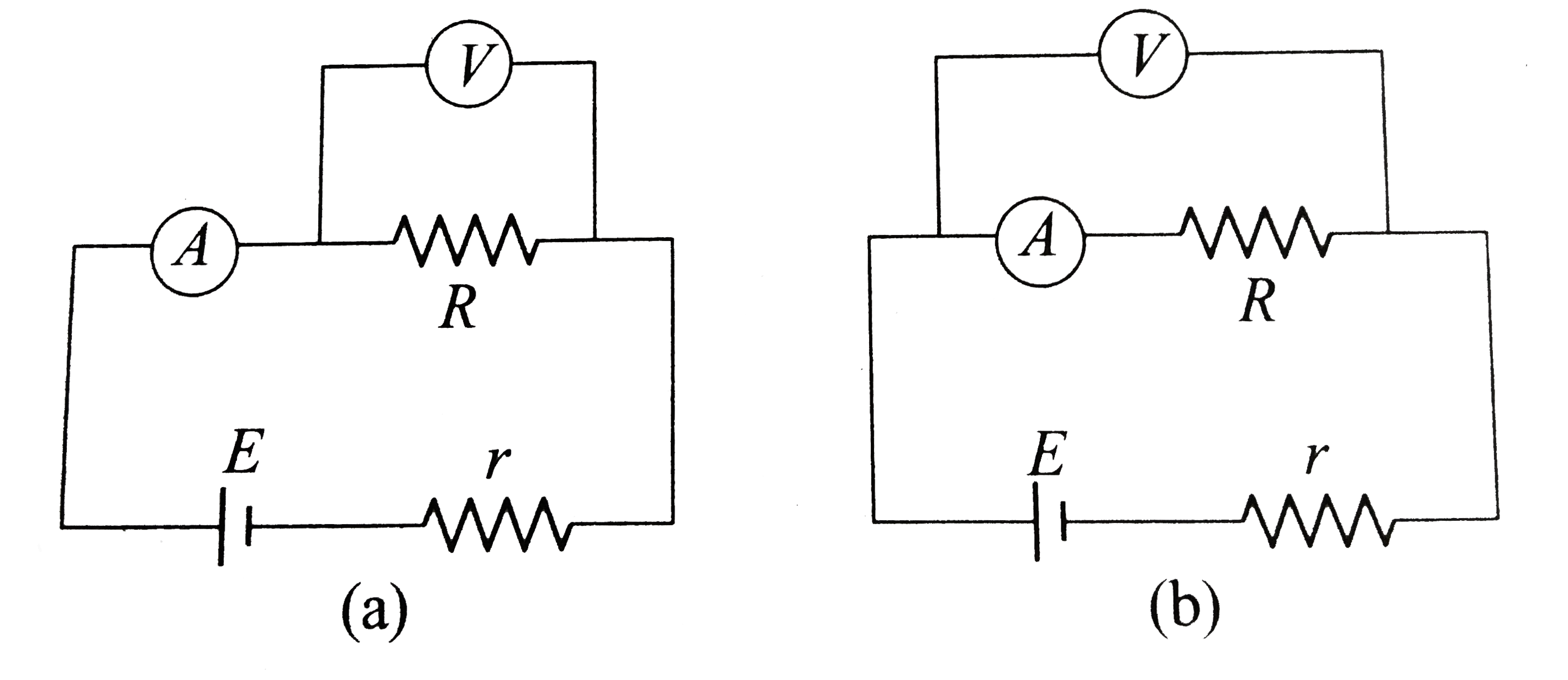 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)is
View SolutionThe resistance of a metal is given by R=V/I , where V is potential difference and I is current . In a circuit , the potential difference across resistance is V=(8±0.5)V and current in resistance , I=(4±0.2)A. What is the value of resistance with its percentage error?
View SolutionIn Ohm's law experiment , the potential drop acros a resistance was as V=5.0V and the current was measured as I=2.00A. Find the maximum permissible error in resistance.
View SolutionIn the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
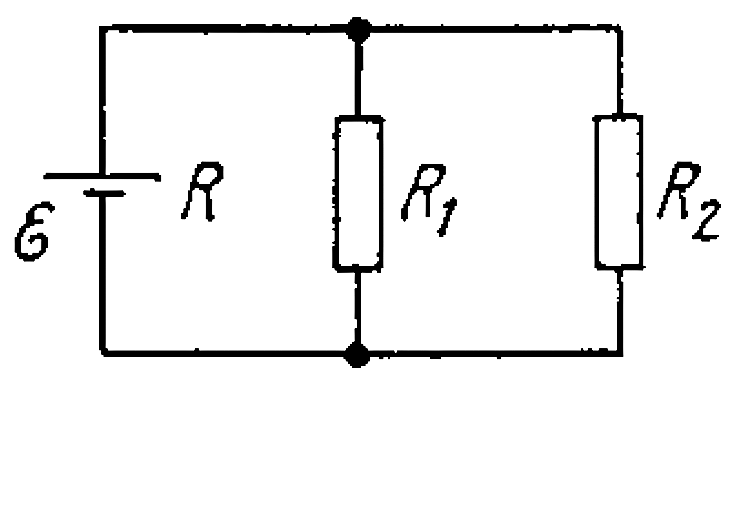
View Solution
