The resistance of a metal is given by , where is potential difference and is current . In a circuit , the potential difference across resistance is and current in resistance , . What is the value of resistance with its percentage error?
The correct Answer is:D
To solve the problem, we need to calculate the resistance R using the formula R=VI, where V is the potential difference and I is the current. We also need to determine the percentage error in the resistance based on the errors in the measurements of V and I.
Step 1: Calculate the resistance R
Given:
- V=8V
- I=4A
Using the formula:
R=VI=8V4A=2Ω
Step 2: Determine the errors in V and I
Given:
- Error in V (denoted as ΔV) = 0.5V
- Error in I (denoted as ΔI) = 0.2A
Step 3: Calculate the relative error in resistance R
The formula for the relative error in R is given by:
ΔRR=ΔVV+ΔII
Substituting the values:
ΔRR=0.58+0.24
Calculating each term:
0.58=0.0625
0.24=0.05
Adding these values together:
ΔRR=0.0625+0.05=0.1125
Step 4: Calculate the absolute error in R
Now, we can find the absolute error ΔR:
ΔR=R×ΔRR=2×0.1125=0.225Ω
Step 5: Calculate the percentage error in R
The percentage error is given by:
Percentage error=(ΔRR)×100=0.1125×100=11.25%
Final Result
Thus, the resistance with its percentage error is:
R=2Ω±11.25%
- V=8V
- I=4A
R=VI=8V4A=2Ω
- Error in V (denoted as ΔV) = 0.5V
- Error in I (denoted as ΔI) = 0.2A
ΔRR=ΔVV+ΔII
ΔRR=0.58+0.24
0.58=0.0625
0.24=0.05
ΔRR=0.0625+0.05=0.1125
ΔR=R×ΔRR=2×0.1125=0.225Ω
Percentage error=(ΔRR)×100=0.1125×100=11.25%
R=2Ω±11.25%
Topper's Solved these Questions
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Multiple Correct
Explore 2 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Linked Comprehension
Explore 3 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Subjective
Explore 31 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Dimensionsal methods provide three major advantages in verification , deviation , and changing the system of units . Any empirical formula that is derived based on this method has to be verified and propportionality constants found by experimental means . The presence or absence of certain factors - non dimensional constants or variables - cannot be identified by this method . So every dimensionally correct relation cannot be taken as perfectly correct.
The time period of oscillation of a drop depends on surface tension σ , density of the liquid ρ , and radius r . The relation is
View SolutionThe accuracy of measurement also lies in the way the results is expressed. The number of digits to which a value is to be expressed is one digit more than number of digits after after an operation is carried out on the given values. The error can be minimised by many trials and using the correct methods are instruments.
If the length and breadth are measured as 4.234and1.05m, the area of the rectangle is
View Solutionαt2=Fv+βx2
Find the dimension formula for [α]and[β] ( here t = time , F = force , v = velocity , x = distance).
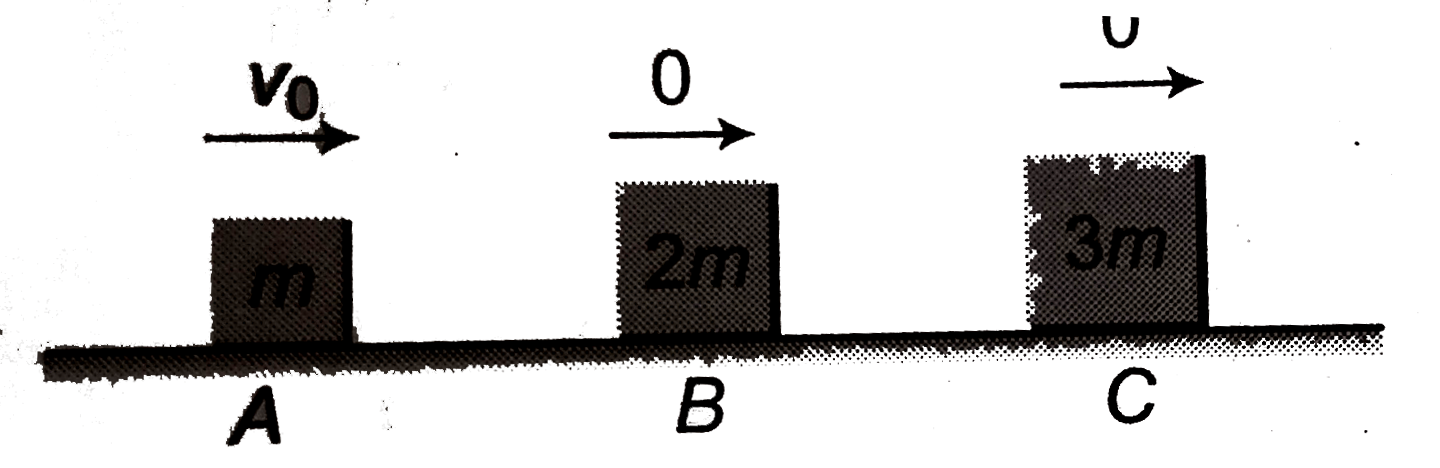
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionA cyclindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed any water is filled in ti upto height H.Now the top is completely sealed with a cap and the orifice at the bottom is opened .Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. The fall in height (in mm) of water level due to opening of the orifice is [ Take atmospheric pressure = 1.0×105Nm2, density of water = 1000kgm3. Neglect any effect of surface tension.]
View SolutionThe resistance R= (V)/(I) , where V= (100+-5.0) V and I=(10+-0.2)A . Find the percentage error in R .
View SolutionThe resistance of a metal is given by R = V//I , where V is potential difference and I is current . In a circuit , the potential difference across resistance is V = ( 8 +- 0.5) V and current in resistance , I = ( 4 +- 0.2)A . What is the value of resistance with its percentage error?
View SolutionIn a circuit potential difference across resistence V=(4±0.25)Vand curent in resistence ,f=(1±0.1) what is the value of resistence with its percentage error
View SolutionThe resistance of metal is given by V = IR , The voltage in the resistance is V = (8 pm 0.5)V and current in the resistance is I = (2 +- 0.2)A , the value fo resistance with its percentage error is
View SolutionIf potential V = 100 +- 0.5 Volt and current I = 10 +- 0.2 amp are given to us. Then what will be the value of resistance
View Solutionप्रतिरोध R = V/I. जहाँ V=(100±5)V एवं I=(10±0.2)A है । R में प्रतिशत त्रुटि ज्ञात कीजिए ।
View Solutionविद्धुत शक्ति से क्या तातपर्य है ?इसका सूत्र
(i)विभान्तर (v)तथा धारा (I),
(ii)धारा(i)तथा प्रतिरोध (R),और
(iii) विभान्तर (V)तथा प्रतिरोध (R)के पदों मे लिखिय
View SolutionThe resistance of a metal is given by R=VI, where V is potential difference and I is the current. In a circuit the potential difference across resistance is V=(8±0⋅5) V and current in resistance, I=(4±0⋅2)A. And current in resistance with its percentage error :
View SolutionThe resistance R= (V)/(I) , where V= (100+-5.0) V and I=(10+-0.2)A . Find the percentage error in R .
View SolutionGive, potential difference V = (8 + 0.5) V and current I = (2 + 0.2) A. The value of resistance R is
View Solution