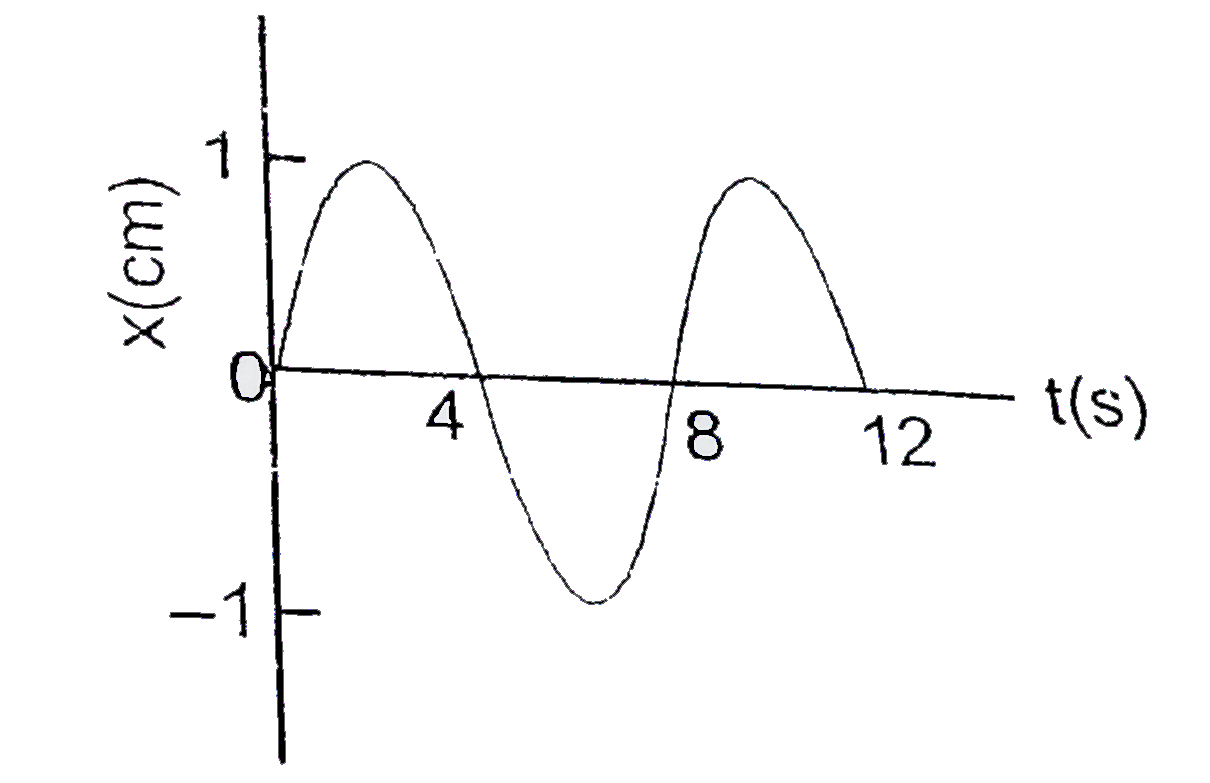
Fig gives the x−t plot of a particle executing one dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particles at t=0.3s, 1.2s,−1.2s,
Negative, Negative, Positive (at t = 0.3 s)
Positive, Positive, Negative (at t = 1.2 s)
Negative, Positive, Positive (at t = –1.2 s)
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a=−w2×w→ angular frequency ... (i)
t=0.3 s
In this time interval, x is negative. Thus, the slope of the x-t plot will also be negative. Therefore, both position and velocity are negative. However, using equation (i), acceleration of the particle will be positive.
t = 1.2 s
In this time interval, x is positive. Thus, the slope of the x–t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative
t = – 1.2 s
In this time interval, x is negative. Thus, the slope of the x–t plot will also be negative. Since both x and t are negative, the velocity comes to be positive. From equation (i), it can be inferred that the acceleration of the particle will be positive.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2The displacement of a particle executing simple harmonic motion is given by y=4sin(2t+ϕ). The period of oscillation is
A2/πBπ/2CπD2π
The x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
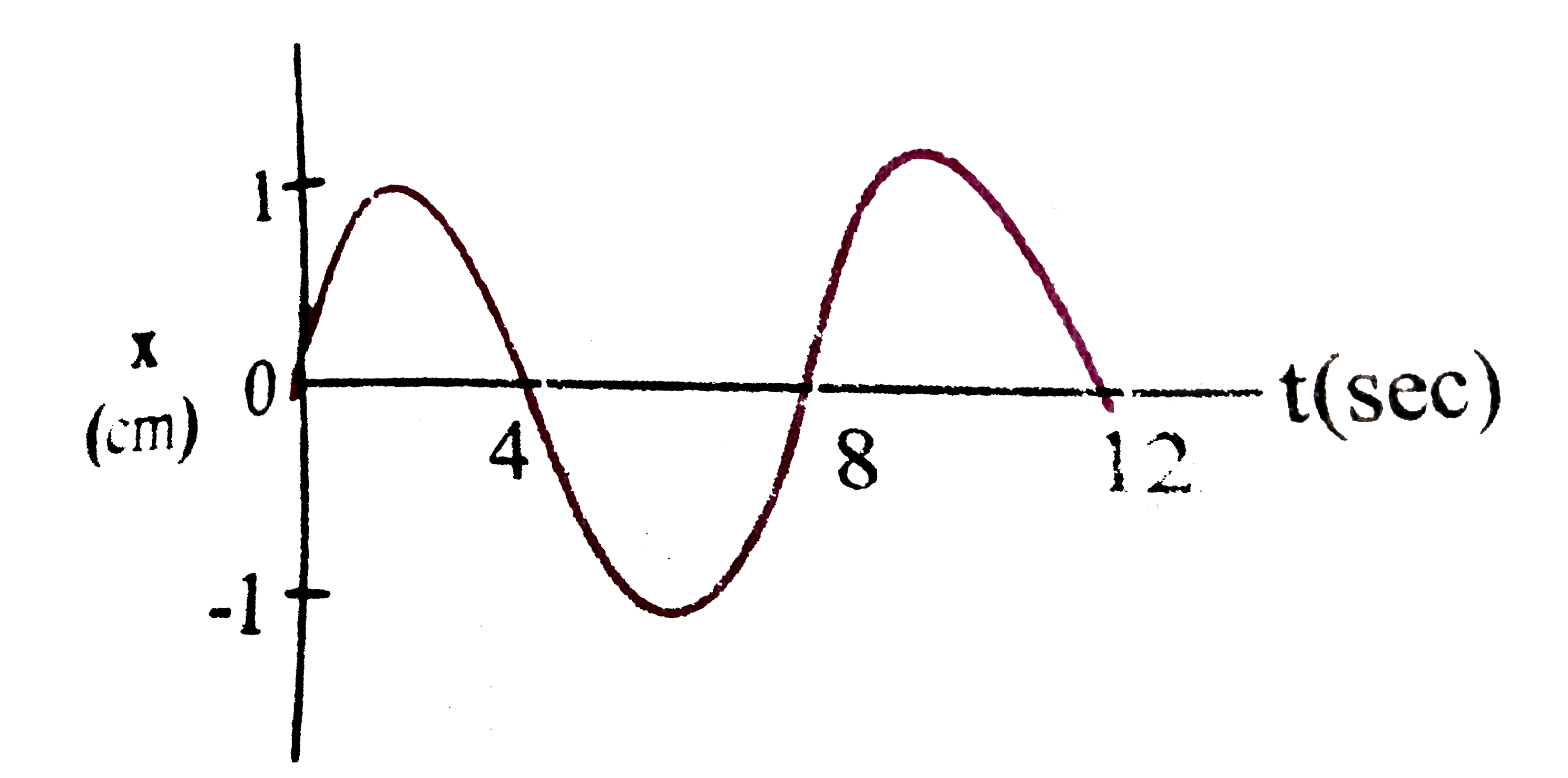
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is

View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionA particle executes simple harmonic motion with an amplitude of 4cm At the mean position the velocity of the particle is 10cm/s. distance of the particle from the mean position when its speed 5 cm/s is
View SolutionThe plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionThe maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm s^-1 and 50 cms^-2. Find the position of the particle when the speed is 8cms^-1.
View Solution