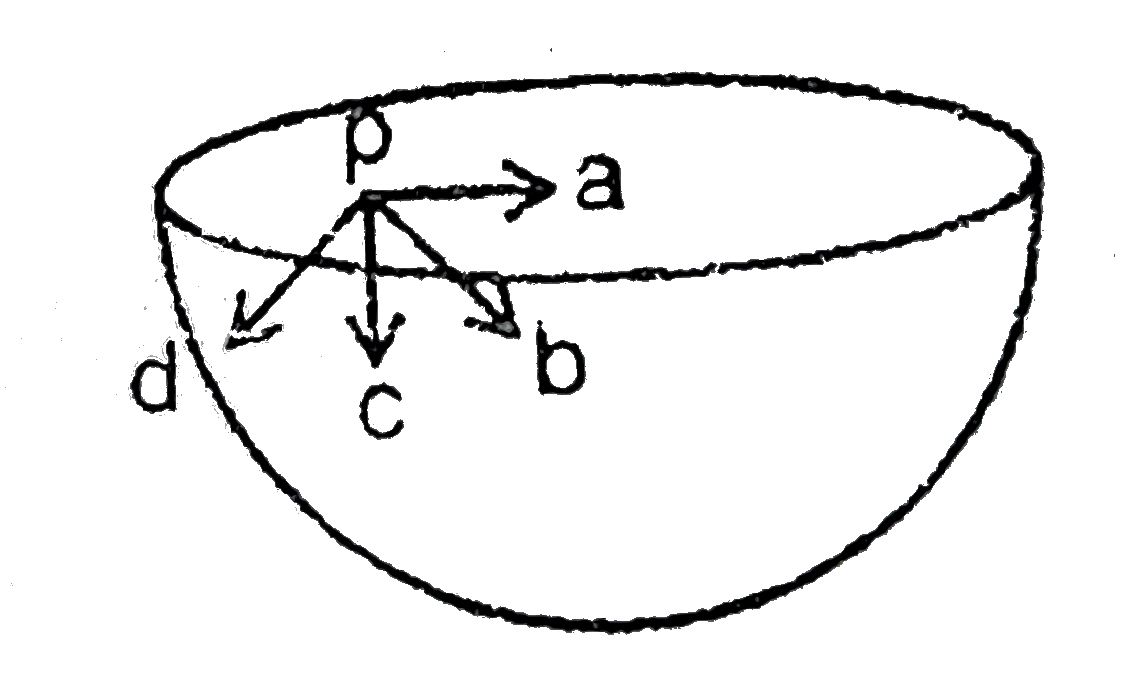
In the following two exercises, choose the correct answer from among the given ones: The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig.) (i) a, (ii) b, (iii) c, (iv) 0.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii), e, (iii) f (iv) g.
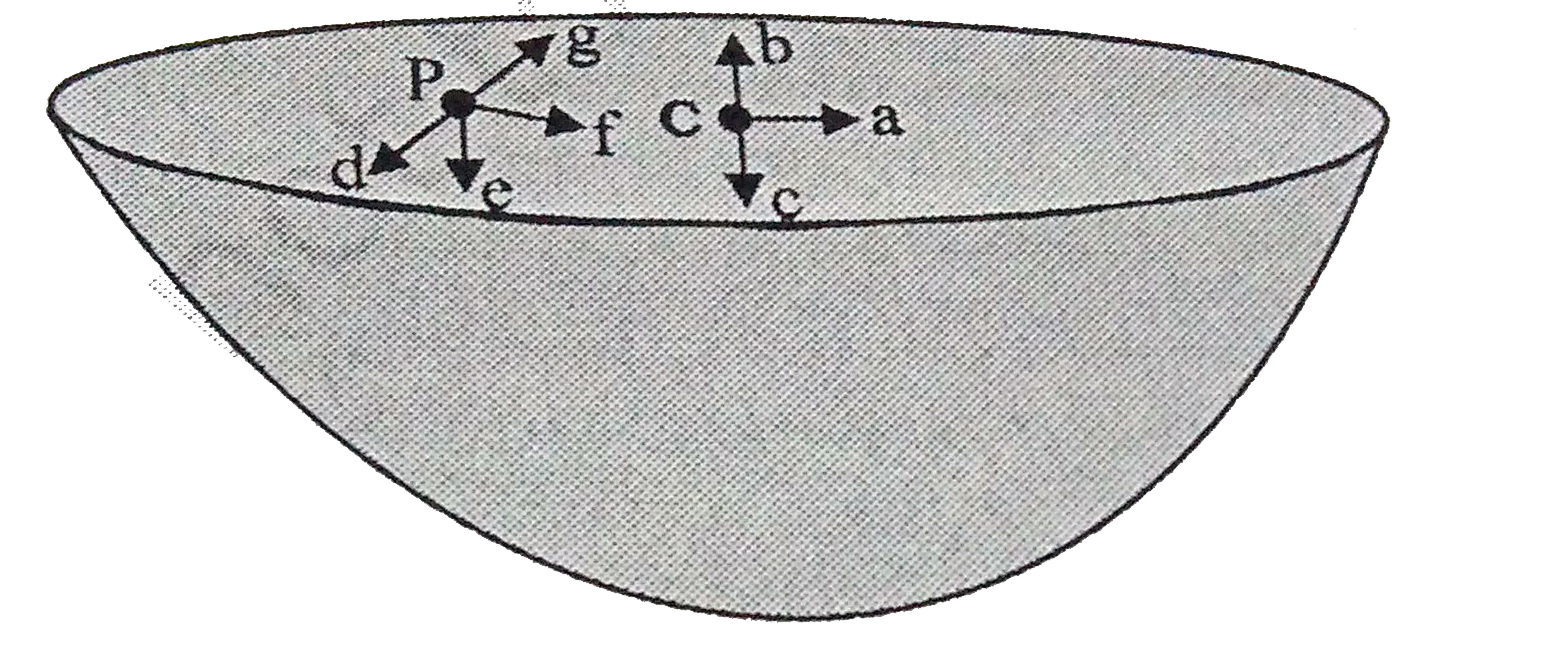
At all points inside a hollow spherical shell, potential is same. So, gravitational intensity, which is negative of gravitational potential gradient, is zero. Due to zero gravitational intensity, the gravitational forces acting on any particle at any point inside a spherical shell will be symmetrically placed. It follows from here that if we remove the upper hemispherical shell, the net gravitational force acting on a particle at P will be downwards. Since gravitational intensity is gravitational force per unit mass therefore, the direction of gravitational intensity will be along c. So, option (iii) is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The direction of gravitational intensity at point P of a hemispherical shell of uniform mass desity is indicated by the arrow
 AdBeCfDg
AdBeCfDg
Calculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionIntensity of gravitational field inside the hollow spherical shell is
View SolutionIdentify the structure indicated by labels (i),(ii),(iii) and (iv) and select the correct option.
View SolutionCalculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)
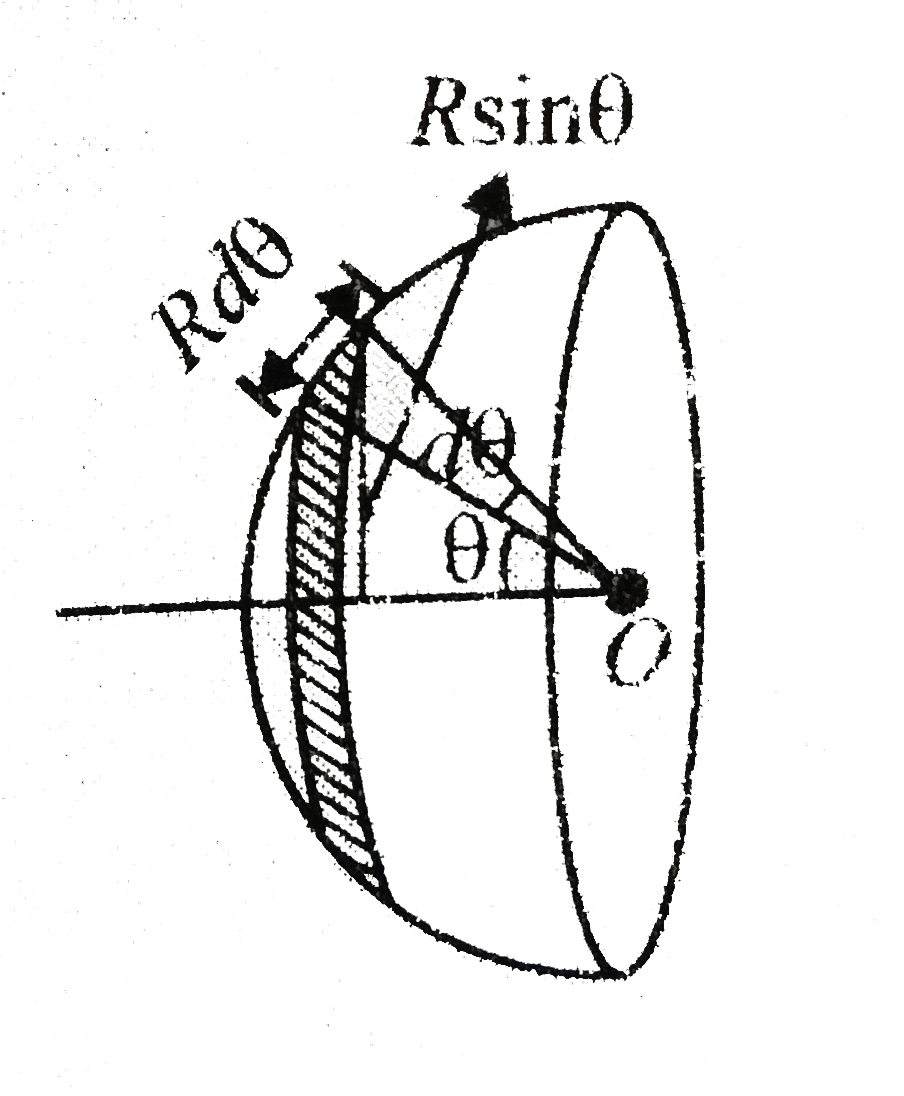
View SolutionA bar magnet is moved in the direction indicated by the arrow between two coil PQ and CD. Predict the directions of induced current in each coil.

View SolutionA bar magnet is moved in the direction indicated by the arrow between two coils PQ and CD. Predict the directions of induced current in each coil.
View SolutionFind ∮→B.→dl over following loops (direction in which integration has to be performed is indicated by arrows)

View Solution


 .
.