Two starts each of one solar mass are approaching each other for a head on collision. When they are a distance km. their speeds are negligible. What is the speed with which they collide? The radius of each star is km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
To solve the problem of two stars colliding, we will use the principle of conservation of energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
- Each star has a mass M=2×1030 kg (solar mass).
- The initial distance between the centers of the two stars is R=109 km, which we convert to meters:
R=109 km=1012 m
- The radius of each star is r=104 km, which we convert to meters:
r=104 km=107 m
Step 2: Calculate the Potential Energy Before Collision
The gravitational potential energy U when the stars are at a distance R is given by:
U=−GM2R
where G=6.67×10−11N m2/kg2.
Step 3: Calculate the Potential Energy After Collision
When the stars collide, the distance between their centers becomes 2r:
U′=−GM22r
Step 4: Calculate the Kinetic Energy After Collision
Let v be the speed of each star at the moment of collision. The kinetic energy K of both stars is:
K=12Mv2+12Mv2=Mv2
Step 5: Apply Conservation of Energy
According to the conservation of energy:
Total Energy Before=Total Energy After
This gives us:
−GM2R=−GM22r+Mv2
Step 6: Rearrange the Equation
Rearranging the equation to solve for v2:
Mv2=−GM2R+GM22r
Factoring out GM2:
v2=GMM(12r−1R)
Thus,
v2=G(12r−1R)
Step 7: Substitute Values
Now substitute the known values:
- G=6.67×10−11
- M=2×1030
- R=1012
- r=107
Calculating:
v2=6.67×10−11(12×107−11012)
=6.67×10−11(12×107−11012)
=6.67×10−11(5×10−8−1×10−12)
=6.67×10−11(5×10−8)
=3.335×10−18
Step 8: Calculate v
Taking the square root:
v=√3.335×10−18≈2.6×106 m/s
Final Answer
The speed with which the stars collide is approximately:
v≈2.6×106 m/s
---
- Each star has a mass M=2×1030 kg (solar mass).
- The initial distance between the centers of the two stars is R=109 km, which we convert to meters:
R=109 km=1012 m
- The radius of each star is r=104 km, which we convert to meters:
r=104 km=107 m
The gravitational potential energy U when the stars are at a distance R is given by:
U=−GM2R
where G=6.67×10−11N m2/kg2.
When the stars collide, the distance between their centers becomes 2r:
U′=−GM22r
Let v be the speed of each star at the moment of collision. The kinetic energy K of both stars is:
K=12Mv2+12Mv2=Mv2
According to the conservation of energy:
Total Energy Before=Total Energy After
This gives us:
−GM2R=−GM22r+Mv2
Rearranging the equation to solve for v2:
Mv2=−GM2R+GM22r
Factoring out GM2:
v2=GMM(12r−1R)
Thus,
v2=G(12r−1R)
Now substitute the known values:
- G=6.67×10−11
- M=2×1030
- R=1012
- r=107
v2=6.67×10−11(12×107−11012)
=6.67×10−11(12×107−11012)
=6.67×10−11(5×10−8−1×10−12)
=6.67×10−11(5×10−8)
=3.335×10−18
Taking the square root:
v=√3.335×10−18≈2.6×106 m/s
The speed with which the stars collide is approximately:
v≈2.6×106 m/s
Topper's Solved these Questions
Similar Questions
Two stars each of 1 solar mass (=2×1030kg) are approaching each other for a head-on collision. When they are at a distance 109km apart their speeds are negligible . What is the speed with which they collide? The radius of each star is 104km. Assume the starts to remain undistorted untile they collide, G=6.67×10−11Nm2kg−2.
View SolutionTwo point charges, each of mass m and charge q are released when they are at a distance d from each other. What is the speed of each charged particle when they are at a distance 2r ?
View Solution
Knowledge Check
Two stars each of mass M and radius R are approaching each other for a head-on collision. They start approaching each other when their separation is r>>R. If their speed at this separation are negligible, the speed v with which they collide would be
Av=√GM(1R−1r)Bv=√GM(12R−1r)Cv=√GM(1R+1r)Dv=√GM(12R+1r)A ship of mass 3×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 3 m. Assuming that the resistance due to water is neglible, what will be the speed of ship ?
A1.5 m/secB60 m/secC0.1 m/secD5m/sec
A source of sound and an observer are approaching each other with the same speed, which is equal to (110) times the speed of sound. The apparent relative change in frequency of source is
View SolutionThe mass ofa star is 3.98×1030 kg and its radius is 106 km. It rotates.about its axis with an angular speed of 10−6 rad/s. Calculate the speed of the star when it collapses to a radius of 104 km ? Assume the moment of inertia of the star to be 25mr2.
View SolutionTwo positively charged particles each of mass is 9×10−30kg and carrying a charge of 1.6×10−19C are placed at a distance .r. apart. If each experiences a force equal to its weight, the value of r is (g=10ms−2)
View SolutionTwo particles one of mass m and the other of mass 2 m are projected horizontally towards each other from the same level above the ground with velocities 10 m/s and 5 m/s respectively . They collide in air and stick to each other . The distance from A , where the combined mass finally land is
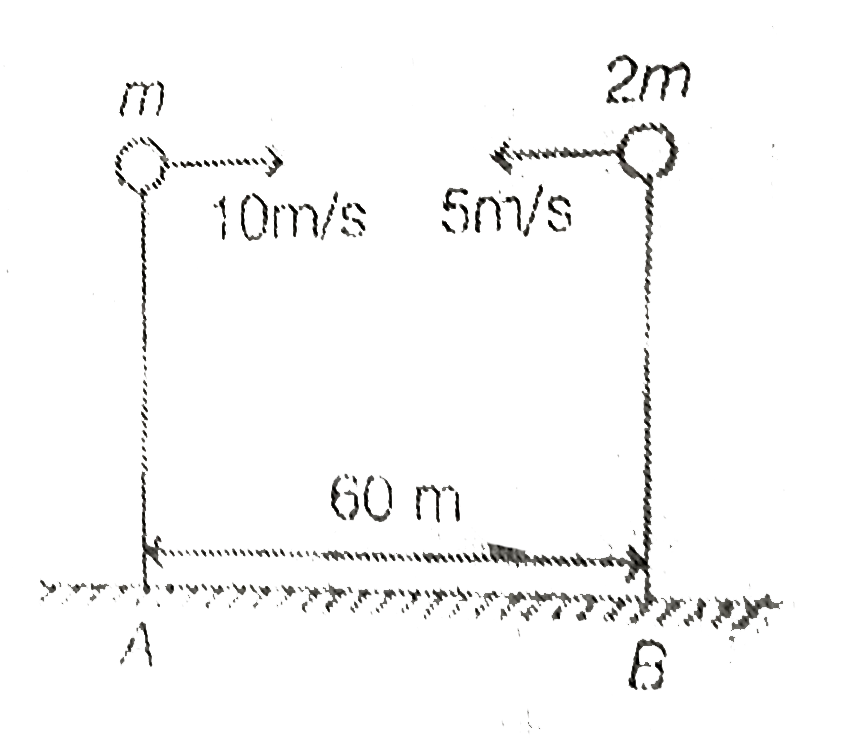
View SolutionA radar sends a signal to an aircraft at a distance of 30 km away and receives it back after 2×10−4 second. What is the speed of the signal ?
View SolutionTwo trains are approaching each other on the same track with velocity 100 km/h and 50 km/h. When they are at a distance of 300 km from each other, a bird starts flying from train 1 towards train 2. When the bird reaches train 2, it instantly reverses its direction and flies again towards train 1. This process continues till the bird is trapped between the trains when they collide. If the bird always travels at a constant speed 200 km/h, the total distance the bird flies is:
View Solution