Two particles each of mass m and speed v, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
To show that the vector angular momentum of the system of two particles is the same about any point taken as the origin, we can follow these steps:
Step 1: Define the system
We have two particles, each of mass m and speed v, moving in opposite directions along parallel lines separated by a distance d.
Step 2: Choose an arbitrary point as the origin
Let’s denote an arbitrary point O as the origin from which we will calculate the angular momentum of the system.
Step 3: Determine the position of the particles
Assume the first particle is moving in the positive direction along its line, and the second particle is moving in the negative direction along its line. Let’s denote the perpendicular distances from point O to the lines of motion of the first and second particles as C1 and C2 respectively.
Step 4: Calculate the angular momentum of each particle
The angular momentum L of a particle about a point is given by the formula:
L = m \cdot v \cdot r_{\perpendicular}
where r_{\perpendicular} is the perpendicular distance from the point to the line of motion.
For the first particle:
L1=m⋅v⋅C2
For the second particle (moving in the opposite direction):
L2=m⋅(−v)⋅C1=−m⋅v⋅C1
Step 5: Total angular momentum of the system
The total angular momentum Ltotal of the system is the sum of the angular momenta of the two particles:
Ltotal=L1+L2=m⋅v⋅C2−m⋅v⋅C1
This can be simplified to:
Ltotal=m⋅v⋅(C2−C1)
Step 6: Relate C2−C1 to d
Since the particles are separated by a distance d, we have:
C2−C1=d
Thus, we can substitute this into our equation for total angular momentum:
Ltotal=m⋅v⋅d
Step 7: Conclusion
The total angular momentum of the system is given by:
Ltotal=m⋅v⋅d
This expression shows that the angular momentum is a constant value that does not depend on the choice of the origin point O. Therefore, the vector angular momentum of this system of particles is the same about any point taken as the origin.
We have two particles, each of mass m and speed v, moving in opposite directions along parallel lines separated by a distance d.
Let’s denote an arbitrary point O as the origin from which we will calculate the angular momentum of the system.
Assume the first particle is moving in the positive direction along its line, and the second particle is moving in the negative direction along its line. Let’s denote the perpendicular distances from point O to the lines of motion of the first and second particles as C1 and C2 respectively.
The angular momentum L of a particle about a point is given by the formula:
L = m \cdot v \cdot r_{\perpendicular}
where r_{\perpendicular} is the perpendicular distance from the point to the line of motion.
L1=m⋅v⋅C2
For the second particle (moving in the opposite direction):
L2=m⋅(−v)⋅C1=−m⋅v⋅C1
The total angular momentum Ltotal of the system is the sum of the angular momenta of the two particles:
Ltotal=L1+L2=m⋅v⋅C2−m⋅v⋅C1
This can be simplified to:
Ltotal=m⋅v⋅(C2−C1)
Since the particles are separated by a distance d, we have:
C2−C1=d
Thus, we can substitute this into our equation for total angular momentum:
Ltotal=m⋅v⋅d
The total angular momentum of the system is given by:
Ltotal=m⋅v⋅d
This expression shows that the angular momentum is a constant value that does not depend on the choice of the origin point O. Therefore, the vector angular momentum of this system of particles is the same about any point taken as the origin.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
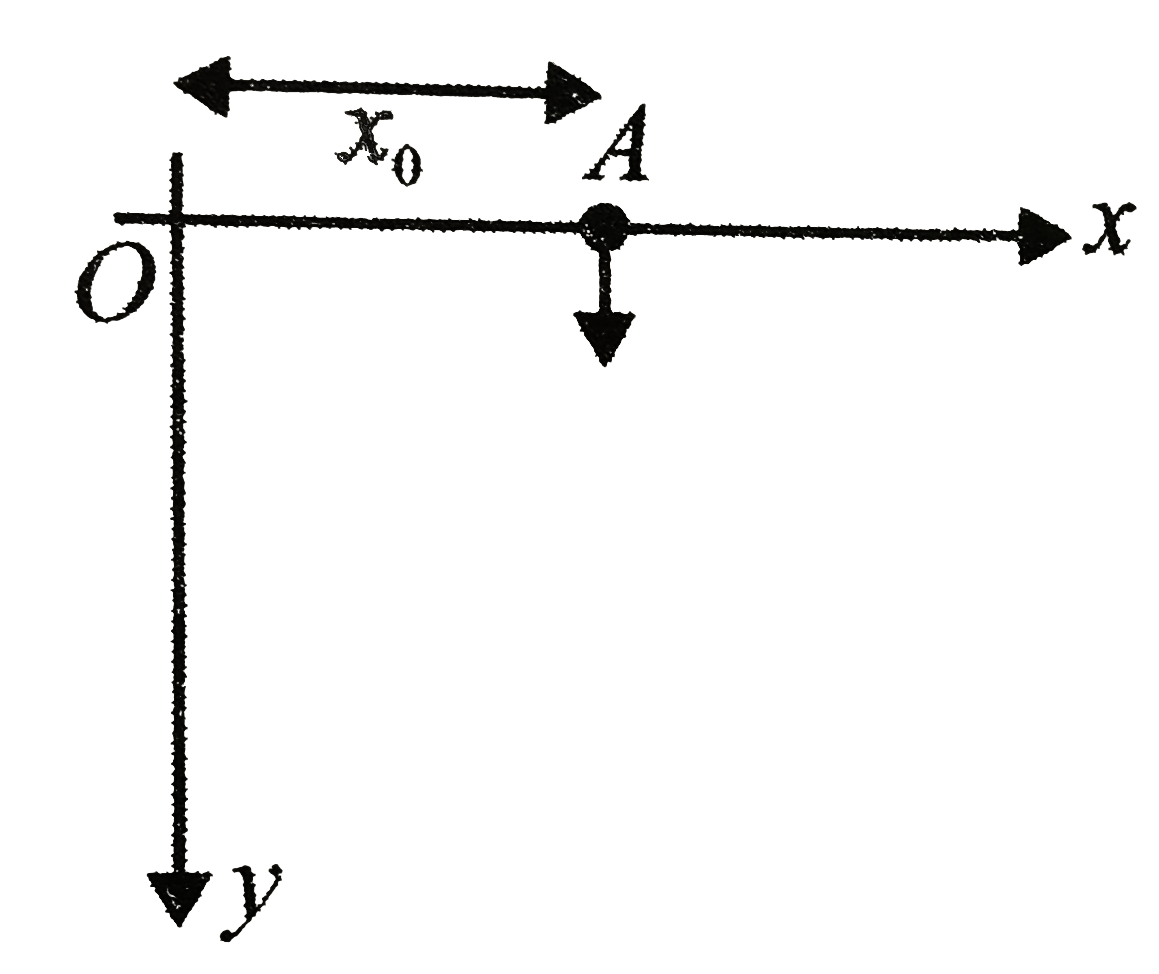
A particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View Solution
Knowledge Check
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
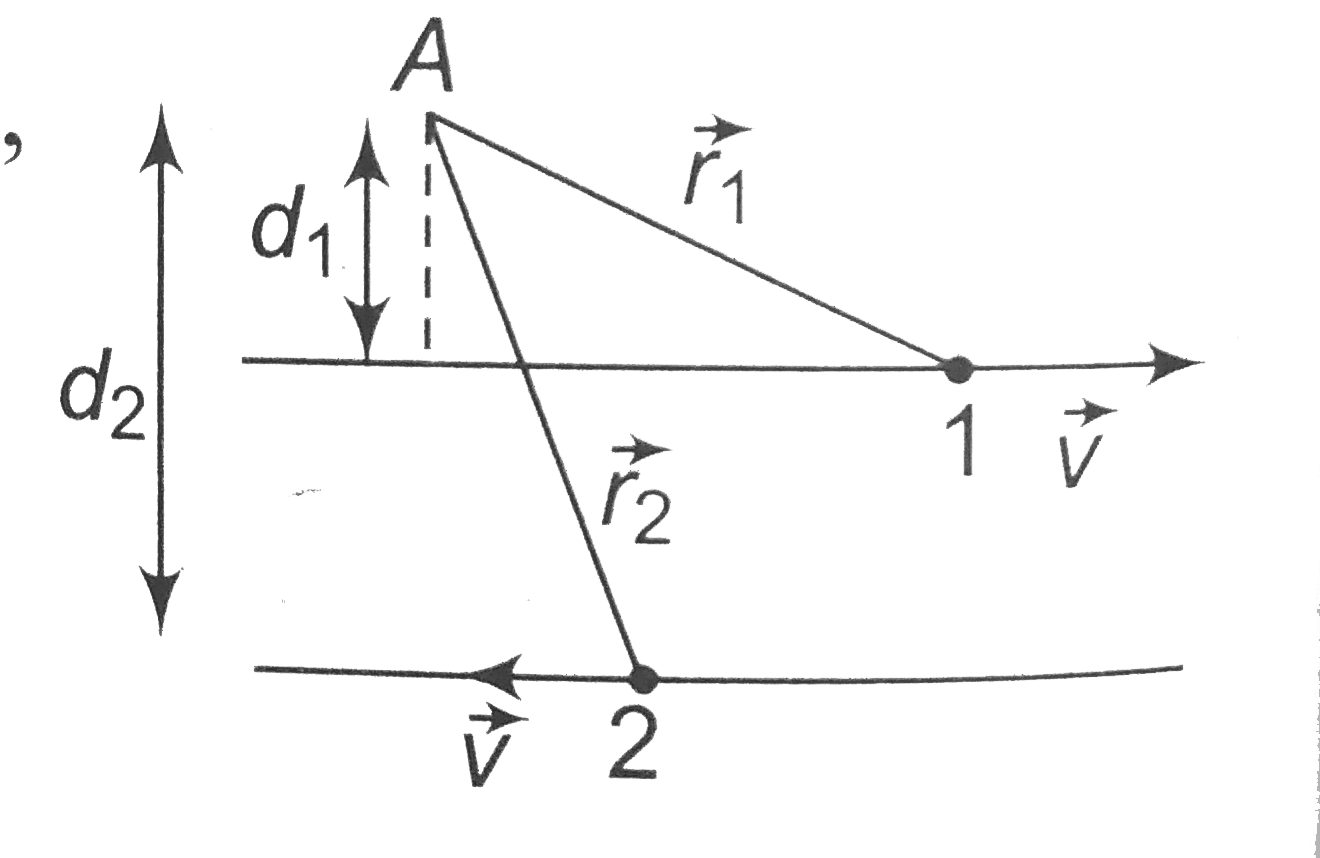 .AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
⊗ represents a unit vector going into the page, ⊙ represent a unit vector coming out of the page
Two particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View SolutionA particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin O

View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionShow that the angular momentum about any point of a single particle moving with constant velocity remains constant throughout the motion.
View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)

View Solution
