In a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to accomplish this task?
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a car lift with two pistons. The first piston has a radius of r1=0.5cm and the second piston has a radius of r2=10.0cm. The mass of the car to be lifted is m=1350kg. We need to find the force F1 exerted by the compressed air on the small piston and the pressure necessary to lift the car.
Step 2: Convert Units
Convert the radius from centimeters to meters:
- r1=0.5cm=0.005m
- r2=10.0cm=0.1m
Step 3: Calculate the Force F2
The force F2 acting on the larger piston due to the weight of the car can be calculated using the formula:
F2=m⋅g
where g (acceleration due to gravity) is approximately 9.8m/s2.
Calculating F2:
F2=1350kg×9.8m/s2=13230N
Step 4: Apply Pascal's Law
According to Pascal's law, the pressure at both pistons is equal:
P1=P2
Pressure is defined as force per unit area:
P1=F1A1andP2=F2A2
Where A1 and A2 are the areas of the pistons:
A1=πr21andA2=πr22
Step 5: Calculate Areas
Calculating the areas:
A1=π(0.005m)2=π(0.000025)≈7.854×10−5m2
A2=π(0.1m)2=π(0.01)≈3.142×10−2m2
Step 6: Set Up the Equation
Since P1=P2:
F1A1=F2A2
Substituting the known values:
F17.854×10−5=132303.142×10−2
Step 7: Solve for F1
Rearranging the equation to find F1:
F1=13230×7.854×10−53.142×10−2
Calculating F1:
F1≈1.039N0.03142≈33.075N
Step 8: Calculate the Pressure
Now we can calculate the pressure P1:
P1=F1A1=33.0757.854×10−5≈421123.97Paor421.12kPa
Final Answers
- The force F1 required to lift the car is approximately 33.075N.
- The pressure necessary to accomplish this task is approximately 421123.97Pa or 421.12kPa.
We have a car lift with two pistons. The first piston has a radius of r1=0.5cm and the second piston has a radius of r2=10.0cm. The mass of the car to be lifted is m=1350kg. We need to find the force F1 exerted by the compressed air on the small piston and the pressure necessary to lift the car.
Convert the radius from centimeters to meters:
- r1=0.5cm=0.005m
- r2=10.0cm=0.1m
The force F2 acting on the larger piston due to the weight of the car can be calculated using the formula:
F2=m⋅g
where g (acceleration due to gravity) is approximately 9.8m/s2.
F2=1350kg×9.8m/s2=13230N
According to Pascal's law, the pressure at both pistons is equal:
P1=P2
Pressure is defined as force per unit area:
P1=F1A1andP2=F2A2
A1=πr21andA2=πr22
Calculating the areas:
A1=π(0.005m)2=π(0.000025)≈7.854×10−5m2
A2=π(0.1m)2=π(0.01)≈3.142×10−2m2
Since P1=P2:
F1A1=F2A2
Substituting the known values:
F17.854×10−5=132303.142×10−2
Rearranging the equation to find F1:
F1=13230×7.854×10−53.142×10−2
Calculating F1:
F1≈1.039N0.03142≈33.075N
Now we can calculate the pressure P1:
P1=F1A1=33.0757.854×10−5≈421123.97Paor421.12kPa
- The force F1 required to lift the car is approximately 33.075N.
- The pressure necessary to accomplish this task is approximately 421123.97Pa or 421.12kPa.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- LAWS OF MOTION BOOK - NCERT ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EXERCISE
40 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
Similar Questions
In a vehicle lifter the enclosed gas exerts a force F on a small piston having a diameter of 8 cm. This pressure is transmitted to a second piston of diameter 24 cm. If the mass of the vehicle to be lifted is 1400 kg then value of F is
View SolutionIf a pressure of 378 atm is exerted on a circular cross section of radius 0.1 mm, what is the force exerted on the area?
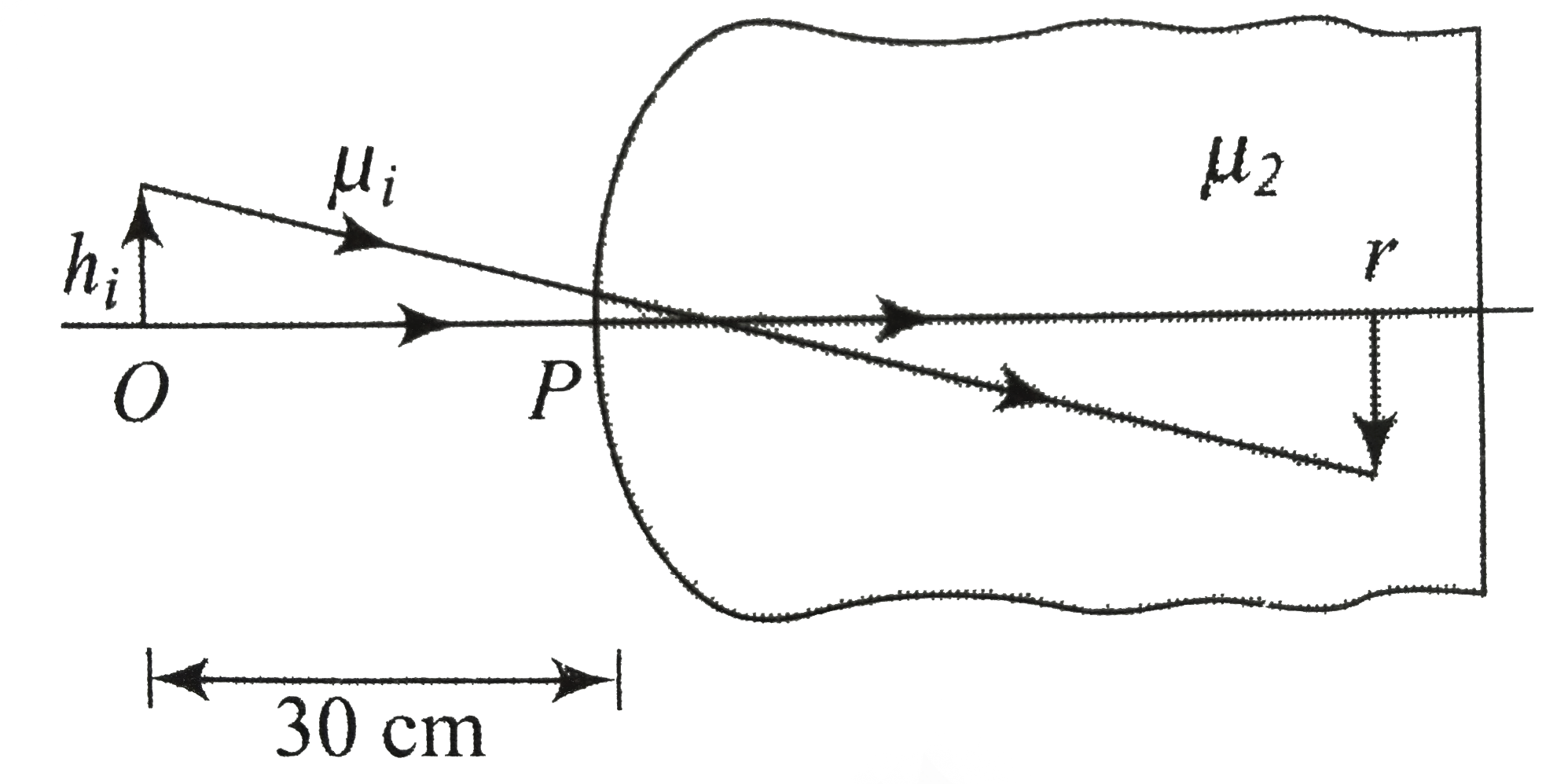
View SolutionA small object of height 0.5 cm is placed in front of a convex surface of glass (μ−1.5) of radius of curvature 10cm. Find the height of the image formed in glass.
View SolutionA disc of mass 5 kg and radius 50 cm rolls on the ground at the rate of 10ms−1. Calculate the K.E. of the disc.
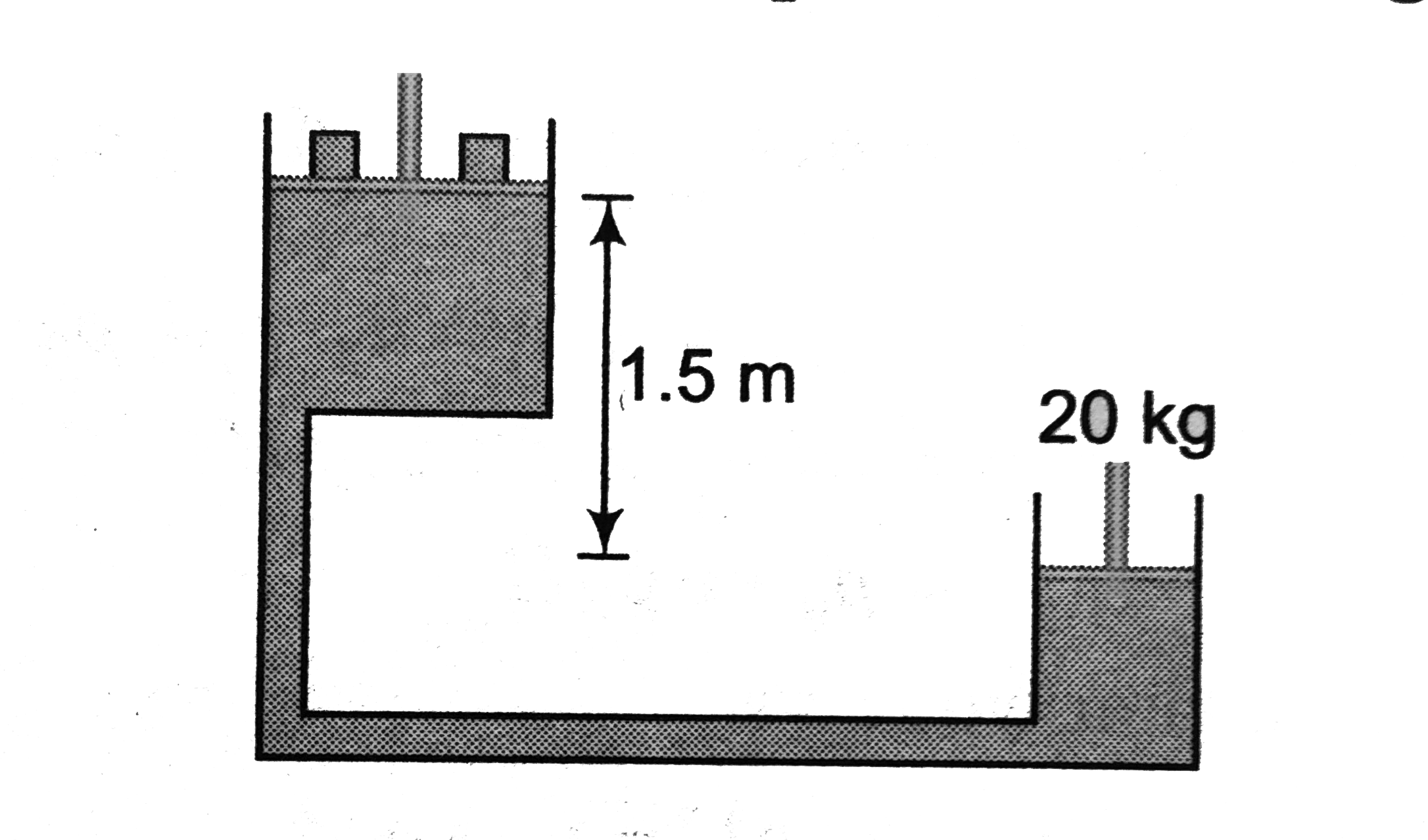
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View SolutionThe radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
View SolutionThe radius of a circular plate increase at the rate of 0.1 cm per second. At what rate does the area increase when the radius of plate is 5πcm?
View SolutionIn a hydraulic lift, used at a service station the radius of the large and small piston are in the ration of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg ?
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View SolutionThe radius of a sphere is measured to be (2.1±0.5) cm. Calculate its surface area with error limits .
View Solution
