In a hydraulic lift, used at a service station the radius of the large and small piston are in the ration of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg ?
3.75 kg
37.5 kg
7.5 kg
75 kg
The correct Answer is:A
To solve the problem of determining the weight that should be placed on the small piston to lift a car of mass 1500 kg using a hydraulic lift, we can follow these steps:
1. Identify the Given Values:
- Mass of the car, m=1500kg
- Radius ratio of the large piston to the small piston, RL:RS=20:1
2. Calculate the Weight of the Car:
- The weight W of the car can be calculated using the formula:
W=m⋅g
- Where g (acceleration due to gravity) is approximately 9.81m/s2.
- Thus,
W=1500kg⋅9.81m/s2=14715N
3. Understanding the Hydraulic Lift Principle:
- In a hydraulic lift, the pressure exerted by the fluid is the same on both pistons. Therefore, we can set up the equation based on pressure:
P1=P2
- Where P1 is the pressure on the small piston and P2 is the pressure on the large piston.
4. Express Pressure in Terms of Force and Area:
- The pressure can be expressed as:
P=FA
- The area A of a piston is given by A=πR2.
- Therefore, we can write:
F1A1=F2A2
5. Substituting Areas:
- Let F1 be the force (weight) on the small piston and F2 be the weight of the car (14715 N).
- The areas can be expressed as:
A1=πR2SandA2=πR2L
- Given the radius ratio RL:RS=20:1, we can express RL=20RS.
6. Calculating the Areas:
- Thus, we have:
A1=πR2SandA2=π(20RS)2=π⋅400R2S
7. Setting Up the Pressure Equation:
- Now, substituting the areas into the pressure equation:
F1πR2S=14715π⋅400R2S
- The πR2S cancels out:
F1=14715400
8. Calculating the Force on the Small Piston:
- Now, calculate F1:
F1=14715400=36.7875N
9. Finding the Equivalent Mass:
- To find the mass equivalent to this force:
m1=F1g=36.78759.81≈3.75kg
Final Answer:
The weight that should be placed on the small piston to lift the car is approximately 3.75 kg.
---
- Mass of the car, m=1500kg
- Radius ratio of the large piston to the small piston, RL:RS=20:1
- The weight W of the car can be calculated using the formula:
W=m⋅g
- Where g (acceleration due to gravity) is approximately 9.81m/s2.
- Thus,
W=1500kg⋅9.81m/s2=14715N
- In a hydraulic lift, the pressure exerted by the fluid is the same on both pistons. Therefore, we can set up the equation based on pressure:
P1=P2
- Where P1 is the pressure on the small piston and P2 is the pressure on the large piston.
- The pressure can be expressed as:
P=FA
- The area A of a piston is given by A=πR2.
- Therefore, we can write:
F1A1=F2A2
- Let F1 be the force (weight) on the small piston and F2 be the weight of the car (14715 N).
- The areas can be expressed as:
A1=πR2SandA2=πR2L
- Given the radius ratio RL:RS=20:1, we can express RL=20RS.
- Thus, we have:
A1=πR2SandA2=π(20RS)2=π⋅400R2S
- Now, substituting the areas into the pressure equation:
F1πR2S=14715π⋅400R2S
- The πR2S cancels out:
F1=14715400
- Now, calculate F1:
F1=14715400=36.7875N
- To find the mass equivalent to this force:
m1=F1g=36.78759.81≈3.75kg
The weight that should be placed on the small piston to lift the car is approximately 3.75 kg.
Similar Questions
In a hydraulic lift at a service station, the radii of the large and small piston are in the ratio of 20 : 1. What weight placed on the small piston will be sufficient to lift a car of mass 1200 kg ?
View SolutionIn a hydraulic machine, the two pistons are of area of cross section in the ratio 1:10. What weight force in needed on the narrow piston to overcome a force of 100 N on the wide piston?
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
View SolutionThe average mass that must be lifted by a hydraulic press is 80kg.If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
View SolutionThe radius of one arm of a hydraulic lift is three times the radius of the other arm. What force should be applied on the narrow arm so as to lift 50 kg at the wider arm?
View SolutionIn a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to accomplish this task?
View SolutionIn a hydraulic press, radii of connecting pipes, r1 and r2 are in the ratio 1:2 . In order to lift a heavy mass M on the larger piston, the small piston must be pressed through a minimum force f equal to
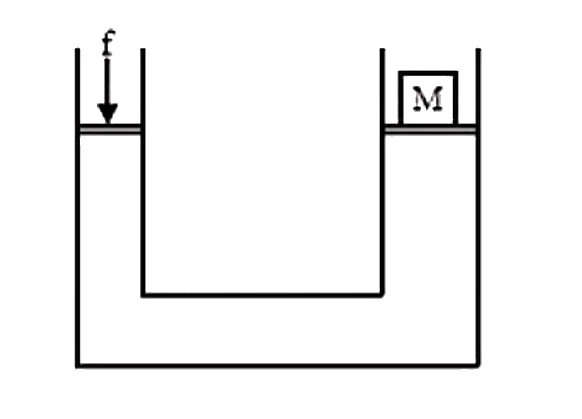
View SolutionIn an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
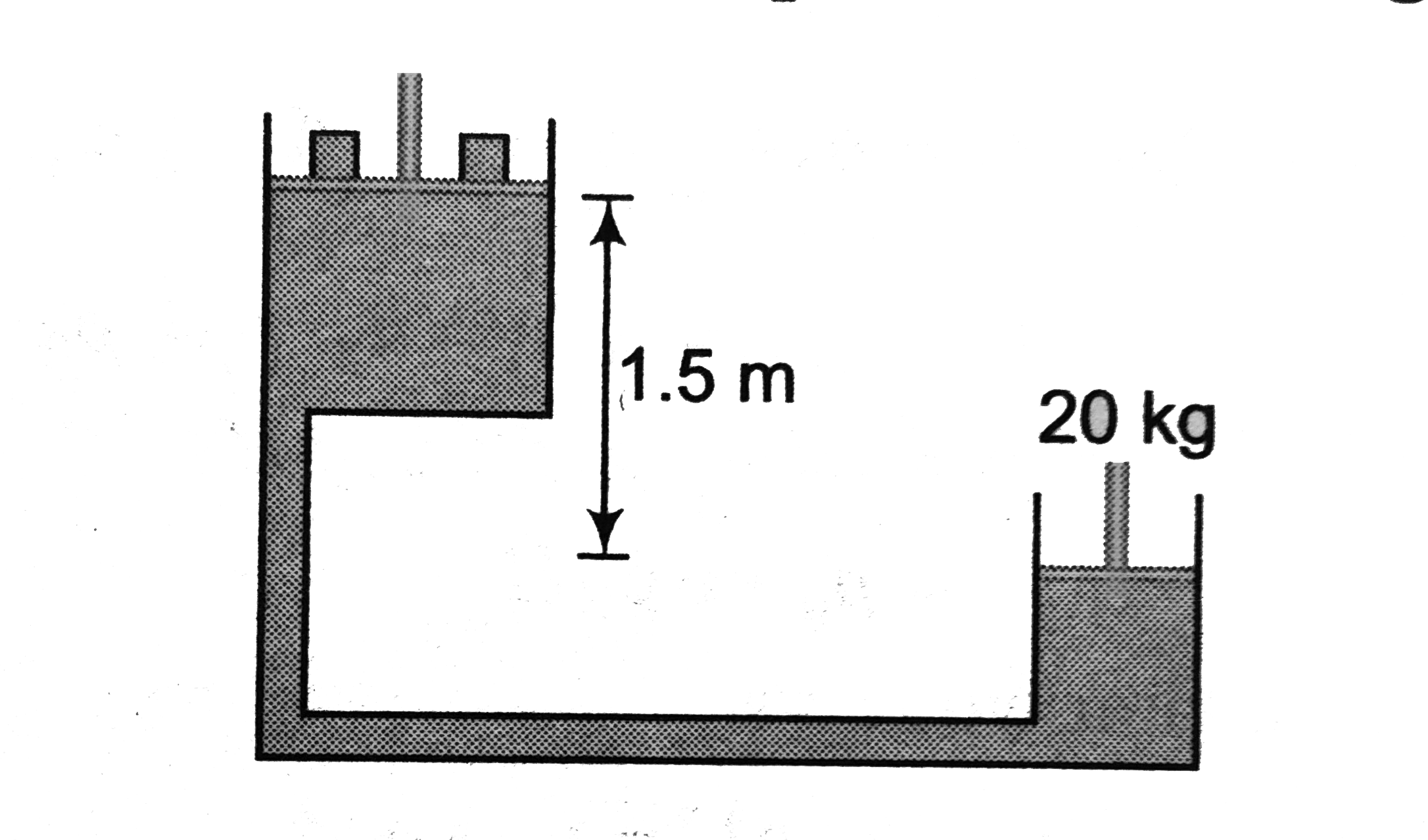 .
.
View Solution
