A network of resistances is connected to a 16 V battery with internal resistance of 1Ω, as shown in Fig. 4.33.

(a) Compute epuivalent resistance of the network,
(b) obtain the current In in each resistor, and
(c ) obtain the voltage drops VAB,VBC and VCD.
(a) The network is a simple series and parallel combination of resistors. First the two 4Ω resistors in parallel are equivalent to a resistor =[(4×4)/(4+4)]Ω=2Ω. In the same way, the 12Ωand6Ω resistors in parallel are equivalent to a resistor of [(12×6)/(12+6)]Ω=4Ω. The equivalent resistance R of the network is obtained by combining these resistors (2Ωand4Ω) with 1Ω in series, that is,
R=2Ω+4Ω+1Ω=7Ω
(b) The total current I in the circuit is
I=εR+r=16V(7+1)Ω=2A
Consider the resistors between A and B. If I2 is the current in one of the 4Ω resistors and I2 the current in the other
I1×4=I2×4
that is, I1=I2, which is otherwise obvious from the symmetry of the two arms. But I1+I2=I=2A. Thus,
I1=I2=1A
that is, current in each 4Ω resistor is 1A. current in 1Ω resistor between B and C would be 2A
Now, consider the resistance between C and D. If I3 is the current in the 12Ω resistor, and I4 in the 6Ω resistor,
I3×12=I4×6 i.e., I4=2I3
But, I3+I4=I=2A
Thus, I3=(23)A,I4=(43)A
that is, the current in the 12Ω resistor is (2/3)A, while the current in the 6Ω resistor is (4/3)A
The voltage drop across AB is
VAB=I1×4=1A×4Ω=4V
This can also be obtained by multiplying the total current between A and B by the equivalent resistance between A and B, that is,
VAB=2A×2Ω=4V
The voltage drop across BC is
VBC=2A×1Ω=2V
Finally, the voltage drop across CD is
VCD=12Ω×I3=12Ω×(23)A=8V
This can alternately be obtained by multiplying total current between C and D by the equivalent resistance between C and D, that is,
VCD=2A×4Ω=8V
Note that the total voltage drop across AD is 4V+2V+8V=14V. Thus, the terminal voltage of the battery is 14 V, while its emf is 16 V. The loss of the voltage (= 2 V) is accounted for by the internal resistance 1Ω of the battery [2A×1Ω=2V].
Topper's Solved these Questions
Similar Questions
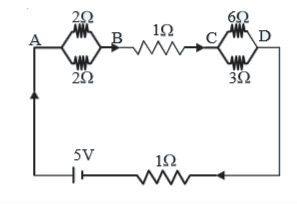
A network of resistors is connected to a 5 V battery with internal resistance of 1Ω as shown in Fig. (a) Compute the equivalent resistance of the network. (6) Obtain the current in each resistor. (c) Obtain the voltage drops VBC and VCD
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View Solution
Knowledge Check
7 V battery with internal resistance 2Ωand3V battery with internal resistance 1Ω are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
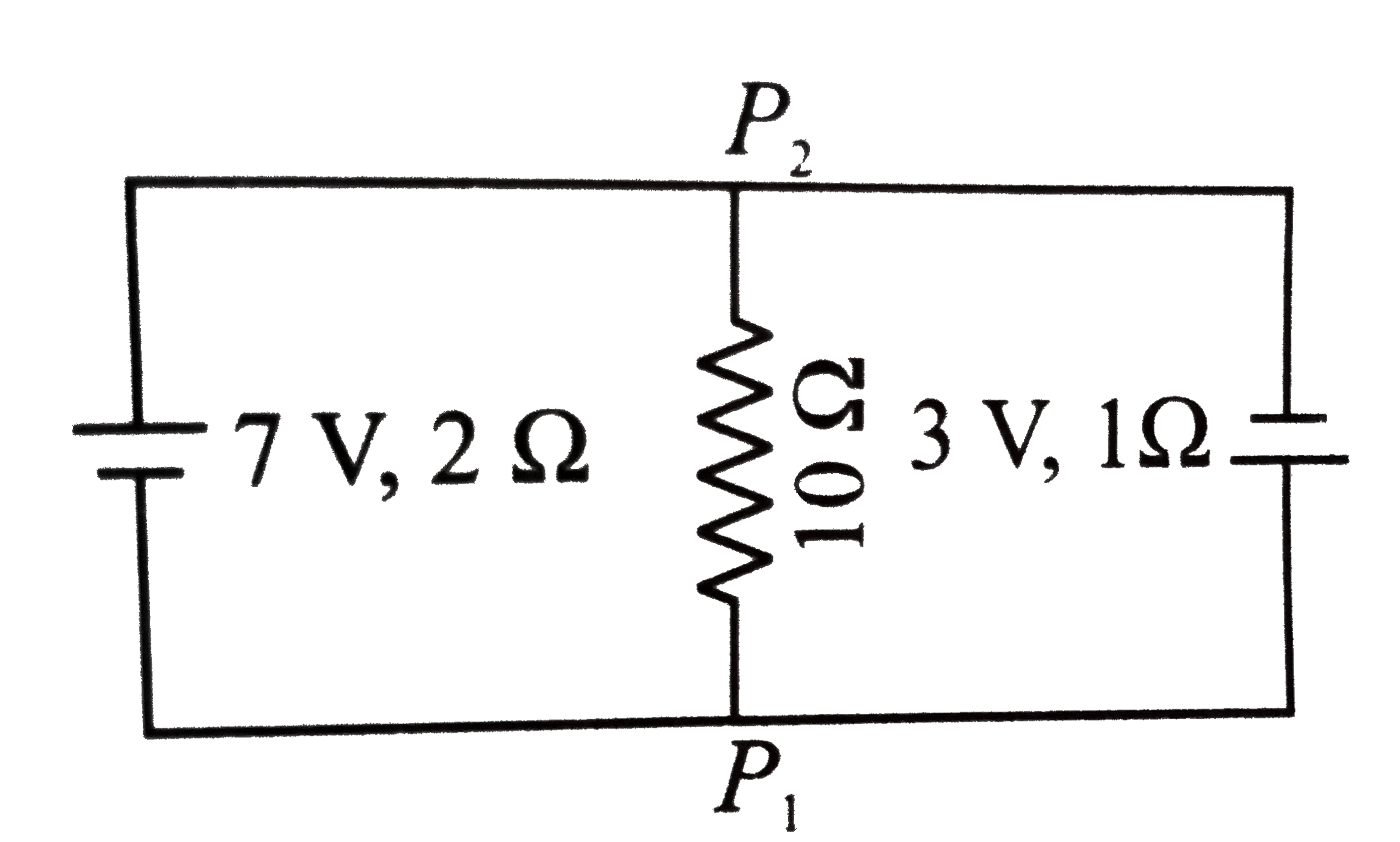 A0.27AB0.31AC0.031AD0.53
A0.27AB0.31AC0.031AD0.53
A network of resistors is connected to a 16V battery as shown in the following figure. Compute the equivalent resistance of the network.
View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
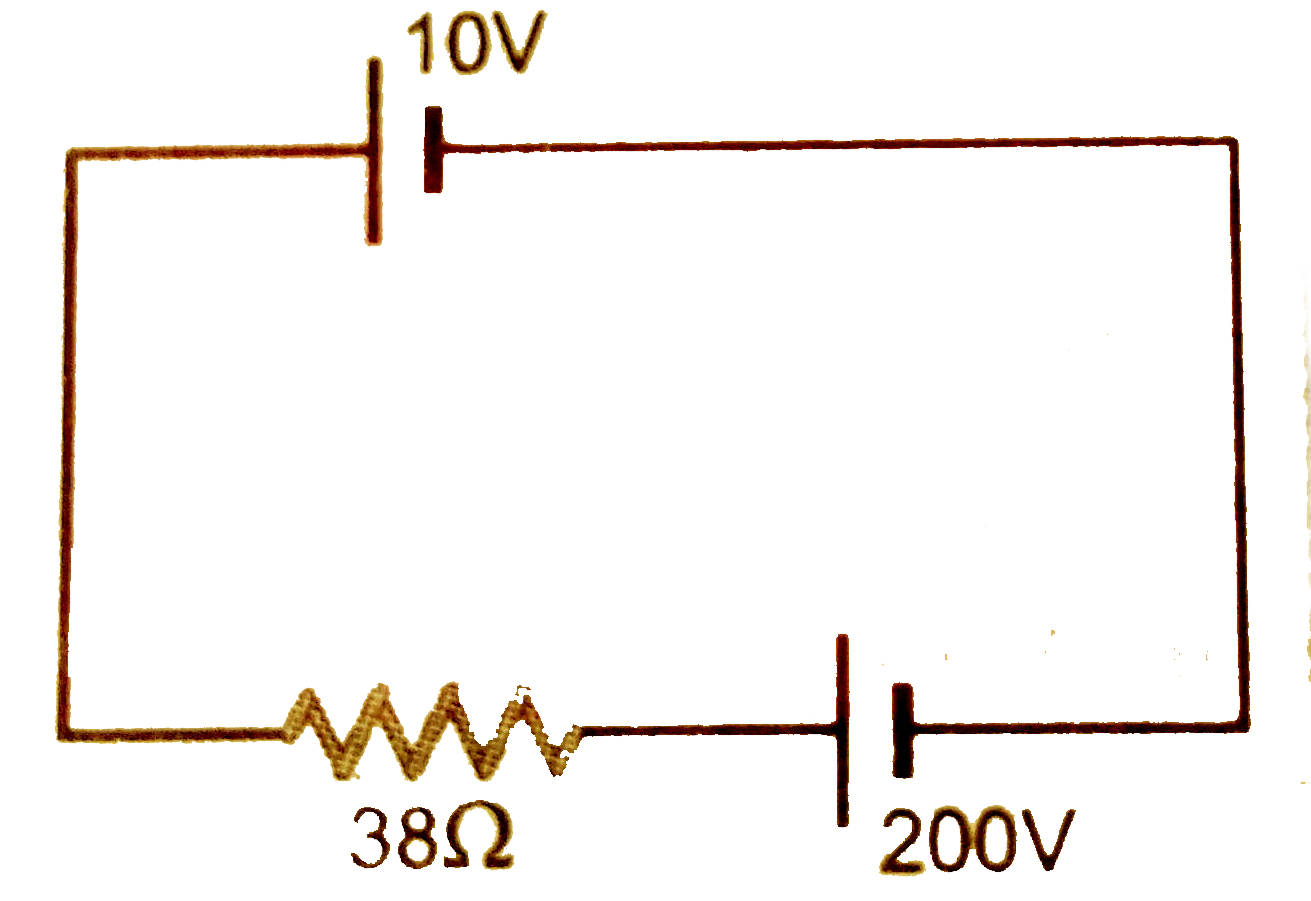 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View SolutionFind the equivalent resistance of the network shown in the figure between the points A and B if
(i) VA>VB (ii) VA<VB

View Solution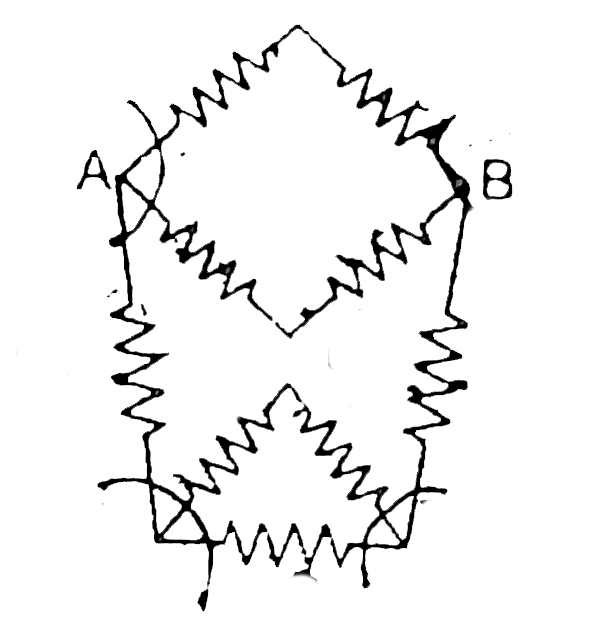
If resistance of each resistor is R then the effective resistance between A&B of the shown network is:
View SolutionA 5 V battery with internal resistance 1Ω and a 2 V battery with internal resistance 0.5Ω are connected to a 3Ω resistor as shown in the figure.The current in the 3Ω resistor is
View SolutionA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor is
View SolutionA battery of internal resistance 4Ω is connected to the network of the resistance as shown in figure . If the maximum power can be delivered to the network, the magnitude of resistance in Ωshould be
View Solution

