A horizontal overhead power lines carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1⋅5m below the line?
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Current (I) = 90 A
- Distance (r) = 1.5 m
- The magnetic field (B) is to be calculated below the power line.
Step 2: Use the formula for the magnetic field due to a straight current-carrying conductor
The magnetic field (B) at a distance (r) from a long straight conductor carrying current (I) is given by the formula:
B=μ0I2πr
where:
- μ0 (the permeability of free space) = 4π×10−7T m/A
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
B=(4π×10−7T m/A)×90A2π×1.5m
Step 4: Simplify the expression
The π terms cancel out:
B=4×10−7×902×1.5
Calculating the denominator:
2×1.5=3
Now substituting back:
B=4×10−7×903
Step 5: Calculate the value
Calculating the numerator:
4×90=360
Thus,
B=360×10−73=120×10−7=1.2×10−5T
Step 6: Determine the direction of the magnetic field
Using the right-hand thumb rule:
- Point your thumb in the direction of the current (east to west).
- Your fingers will curl around the wire in the direction of the magnetic field.
Since the point of interest is below the wire, the fingers will point downwards, indicating that the magnetic field direction is towards the south.
Final Answer
The magnitude of the magnetic field is 1.2×10−5T and its direction is towards the south.
---
- Current (I) = 90 A
- Distance (r) = 1.5 m
- The magnetic field (B) is to be calculated below the power line.
The magnetic field (B) at a distance (r) from a long straight conductor carrying current (I) is given by the formula:
B=μ0I2πr
where:
- μ0 (the permeability of free space) = 4π×10−7T m/A
Substituting the known values into the formula:
B=(4π×10−7T m/A)×90A2π×1.5m
The π terms cancel out:
B=4×10−7×902×1.5
Calculating the denominator:
2×1.5=3
Now substituting back:
B=4×10−7×903
Calculating the numerator:
4×90=360
Thus,
B=360×10−73=120×10−7=1.2×10−5T
Using the right-hand thumb rule:
- Point your thumb in the direction of the current (east to west).
- Your fingers will curl around the wire in the direction of the magnetic field.
The magnitude of the magnetic field is 1.2×10−5T and its direction is towards the south.
Topper's Solved these Questions
Similar Questions
Find the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionA long straight wire in the horizontal plane carries a current of 50A in north to south direction. Give the magnitude and direction of →B at a point 2⋅5m east of the wire.
View Solution
Knowledge Check
A long straight wire in the horizontal plane carries as curret of 75 A in north to south direction, magnitude and direction of field B at a point 3 m east of the wire is
A4×10−6T, vertical upB5×10−6T, vertical downC5×10−6T, vertical upD4×10−6T, vertical down
An electric current flows in a wire from north to south.
What will be the direction of the magnetic field due to this wire at a point.
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (vec B)due to this current.
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionA copper wire of diameter 1.6 mm carries a current of 20A. Find the maximum magnitude of the magnetic field (→B) due to this current.
View SolutionTwo similar coaxial coils, separated by some distance, carry the same current I but in opposite directions. The magnitude of the magnetic field B at a point on the axis at the mid point of the line joining the centre is :
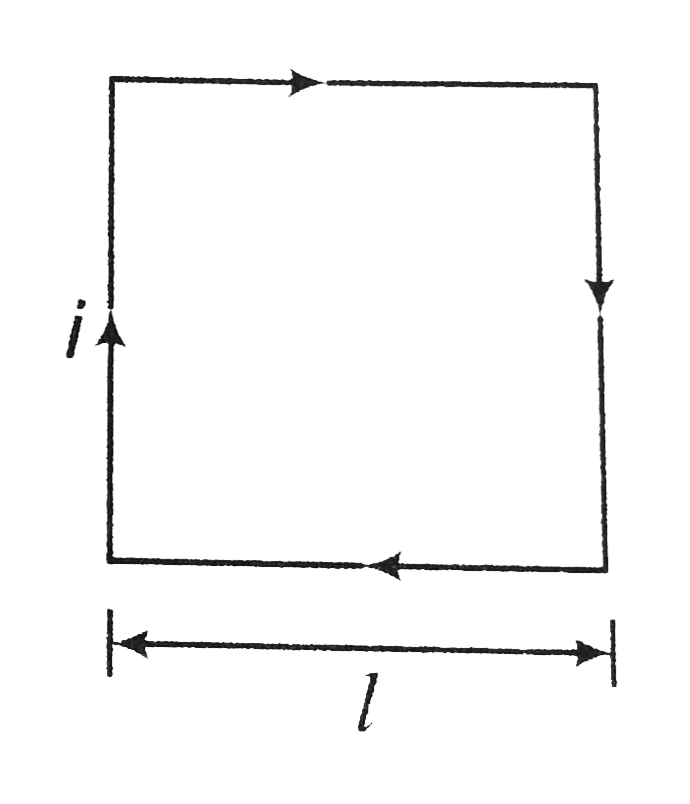
View Solutiona. A conductor in the shape of a square of edge length l=0.4m carries a current i=10.0A. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.
View SolutionIn the circuit diagram show below, the magnitude and direction of the flow of current respectively would be -
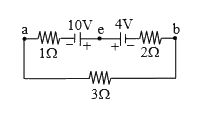
View Solution
