If the bar magnet in the above problem is turned around by 180∘, where will the new null points be located?
To find the new null points when a bar magnet is turned around by 180 degrees, we can follow these steps:
1. Understand the Initial Setup:
- In the previous problem, we had a bar magnet oriented horizontally with its North pole pointing in a specific direction. The Earth’s magnetic field is also present, which influences the magnetic field created by the bar magnet.
2. Turn the Bar Magnet:
- When the bar magnet is turned 180 degrees, the North pole now points in the opposite direction, and the South pole also switches places. This means the orientation of the bar magnet changes, affecting the direction of the magnetic field it produces.
3. Identify the Magnetic Field Directions:
- The magnetic field of the bar magnet will now point from the South pole to the North pole. The Earth’s magnetic field remains unchanged in direction.
4. Determine the Null Points:
- The null points (points where the magnetic field is zero) occur where the magnetic field due to the bar magnet cancels out the Earth’s magnetic field.
- For a bar magnet, the null points are located along the equatorial line, which is perpendicular to the magnetic axis of the magnet.
5. Set Up the Equations:
- Let B1 be the magnetic field due to the bar magnet at distance d1 from the center of the magnet before it was turned.
- Let B2 be the magnetic field at distance d2 after the magnet is turned.
- The equations for the magnetic fields are:
B1=μ04π⋅2md31(before turning)
B2=μ04π⋅md32(after turning)
6. Equate the Magnetic Fields:
- At the null point, B1=B2:
μ04π⋅2md31=μ04π⋅md32
- Simplifying this gives:
2d31=1d32
7. Solve for d2:
- Rearranging gives:
d32=d312
d2=(d312)1/3=d121/3
8. Substituting the Value of d1:
- If d1=14 cm (from the previous problem), we substitute this value:
d2=14cm21/3≈11.0cm
Conclusion:
The new null point after turning the bar magnet by 180 degrees will be located approximately 11.0 cm from the center of the magnet.
- In the previous problem, we had a bar magnet oriented horizontally with its North pole pointing in a specific direction. The Earth’s magnetic field is also present, which influences the magnetic field created by the bar magnet.
- When the bar magnet is turned 180 degrees, the North pole now points in the opposite direction, and the South pole also switches places. This means the orientation of the bar magnet changes, affecting the direction of the magnetic field it produces.
- The magnetic field of the bar magnet will now point from the South pole to the North pole. The Earth’s magnetic field remains unchanged in direction.
- The null points (points where the magnetic field is zero) occur where the magnetic field due to the bar magnet cancels out the Earth’s magnetic field.
- For a bar magnet, the null points are located along the equatorial line, which is perpendicular to the magnetic axis of the magnet.
- Let B1 be the magnetic field due to the bar magnet at distance d1 from the center of the magnet before it was turned.
- Let B2 be the magnetic field at distance d2 after the magnet is turned.
- The equations for the magnetic fields are:
B1=μ04π⋅2md31(before turning)
B2=μ04π⋅md32(after turning)
- At the null point, B1=B2:
μ04π⋅2md31=μ04π⋅md32
- Simplifying this gives:
2d31=1d32
- Rearranging gives:
d32=d312
d2=(d312)1/3=d121/3
- If d1=14 cm (from the previous problem), we substitute this value:
d2=14cm21/3≈11.0cm
The new null point after turning the bar magnet by 180 degrees will be located approximately 11.0 cm from the center of the magnet.
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise
25 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise
37 Videos
- MOVING CHARGES AND MANGNETISM BOOK - NCERT ENGLISHCHAPTER - MOVING CHARGES AND MANGNETISM EXERCISE - Exercise
28 Videos
Similar Questions
When the N-pole of a bar magnet points towards the south and S-pole towards the north, the null points are at the
View SolutionA short bar magnet is placed along N-S direction with N pole pointing north. The neutral points are located 20 cm away from the bar magnet. If BH is the horizontal component of earth's magnetic field then the magnetic field due to the bar magnet at distance of 40 cm along its axis is
View Solution
Knowledge Check
A compass needle free to turn in a horizontal plane is placed at the centre of a circular coil of 30turns and radius 12cm. The coil is in a vertical plane malting an angle of 45∘ with the magnetic meridian when the current in the coil is 0.35A, the needle points west to east. Determine the horizontal component of earth's magnetic field at the location.
A3.9×10−7teslaB3.9×105teslaC8.0×10−5teslaD7.0×10−7teslaThe time period of oscillation of a bar magnet suspended horizontaliy along the magnetic meridian is T0. If this magnet is replaced by another magnet of the same size and pole strength but with double the mass, the new time period will be
AT02BT0√2C√2T0D2T0
A small magnetic needle performs 10 oscillations/minute in the earth's horizontal magnetic field . When a bar magnet is placed near the small magnet in same position , frequency of oscillations becomes 10√2 oscillations/minute . If the bar magnet be turned around end to end , the rate of oscillation of small magnet will become
View SolutionA short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14cm from the centre of the magnet. The earth's magnetic field at the plane is 0⋅36G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null points (i.e. 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and apposite to the horizontal component of earth's magnetic field).
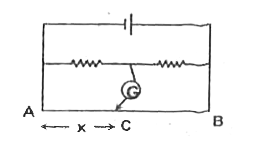
View SolutionIn the meter bridge circuit shown, the null point is obtained at C(AC=x) on the wire AB. If the diameter of the wire AB is doubled, the position of the new null point C' will correspond to
View SolutionDraw magnetic field lines around a bar magnet.
View SolutionDraw magnetic field lines around a bar magnet.
View SolutionA thin bar magnet has dipole moment M . If this is bent in the form of semicircle , then find the new dipole moment .
View Solution
