The 6563ÅH2 line emitted by hydrogen in a star is found to be red shifted by 15Å. Estimate the speed with which the star is receding from earth.
To solve the problem of estimating the speed with which the star is receding from Earth based on the redshift of the H₂ line, we can follow these steps:
Step 1: Identify the Given Values
We have the following values:
- Original wavelength of the H₂ line, λ=6563Å
- Redshift in wavelength, Δλ=15Å
Step 2: Calculate the Observed Wavelength
The observed wavelength λ′ can be calculated as:
λ′=λ+Δλ
Substituting the values:
λ′=6563Å+15Å=6578Å
Step 3: Use the Redshift Formula
The formula relating the change in wavelength to the speed of the star is given by:
Δλλ=VC
Where:
- V is the speed of the star,
- C is the speed of light (C≈3×108m/s).
Step 4: Rearrange the Formula for Speed
We can rearrange the formula to solve for V:
V=C⋅Δλλ
Step 5: Substitute the Values
Now we substitute the known values into the equation. First, we need to convert the wavelengths from Ångströms to meters:
- λ=6563Å=6563×10−10m
- Δλ=15Å=15×10−10m
Now substituting these into the equation:
V=3×108m/s⋅15×10−10m6563×10−10m
Step 6: Calculate the Speed
Calculating the fraction:
156563≈0.002287
Now substituting this back into the equation for V:
V≈3×108m/s⋅0.002287≈686,000m/s
Thus, the speed of the star receding from Earth is approximately:
V≈6.86×105m/s
Step 7: Interpret the Result
The negative sign in the velocity indicates that the star is moving away from the Earth.
Final Answer
The speed with which the star is receding from Earth is approximately 6.86×105m/s.
---
We have the following values:
- Original wavelength of the H₂ line, λ=6563Å
- Redshift in wavelength, Δλ=15Å
The observed wavelength λ′ can be calculated as:
λ′=λ+Δλ
Substituting the values:
λ′=6563Å+15Å=6578Å
The formula relating the change in wavelength to the speed of the star is given by:
Δλλ=VC
Where:
- V is the speed of the star,
- C is the speed of light (C≈3×108m/s).
We can rearrange the formula to solve for V:
V=C⋅Δλλ
Now we substitute the known values into the equation. First, we need to convert the wavelengths from Ångströms to meters:
- λ=6563Å=6563×10−10m
- Δλ=15Å=15×10−10m
V=3×108m/s⋅15×10−10m6563×10−10m
Calculating the fraction:
156563≈0.002287
Now substituting this back into the equation for V:
V≈3×108m/s⋅0.002287≈686,000m/s
Thus, the speed of the star receding from Earth is approximately:
V≈6.86×105m/s
The negative sign in the velocity indicates that the star is moving away from the Earth.
The speed with which the star is receding from Earth is approximately 6.86×105m/s.
Topper's Solved these Questions
Similar Questions
The 6563 Å line emitted by hydrogen atom in a star is found to be red shifted by 5 Å. The speed with which the star is receding form the earth is
View SolutionA 6000 Å Hβ line emitted by hydrogen in a star is observed to be red shifted by 10 Å. Find the speed with which star is receding away from the earth.
View SolutionThe wavelength of Hα line in the hydrogen spectrum is found to be 6563Å in the laboratory. If the velocity of the milky way is 1.05×106ms−1, then the wavelength of Hα line in the spectrum of milky way will be
View SolutionIn hydrogen spectrum the wavelength of Ha line is 656nm, where in the spectrum of a distance galaxy Ha line wavelength is 706nm . Estimated speed of the galaxy with respect to earth is ,
View SolutionIn hydrogen spectrum the wavelength of Ha line is 656nm, where in the spectrum of a distance galaxy Ha line wavelength is 706nm . Estimated speed of the galaxy with respect to earth is ,
View SolutionThe wavelength of Hα line in hydrogen spectrum was found 6563Å in the laboratory. If the wavelength of same line in the spectrum of a milky way is observed to be 6586Å, then the recessional velocity of the milky way will be
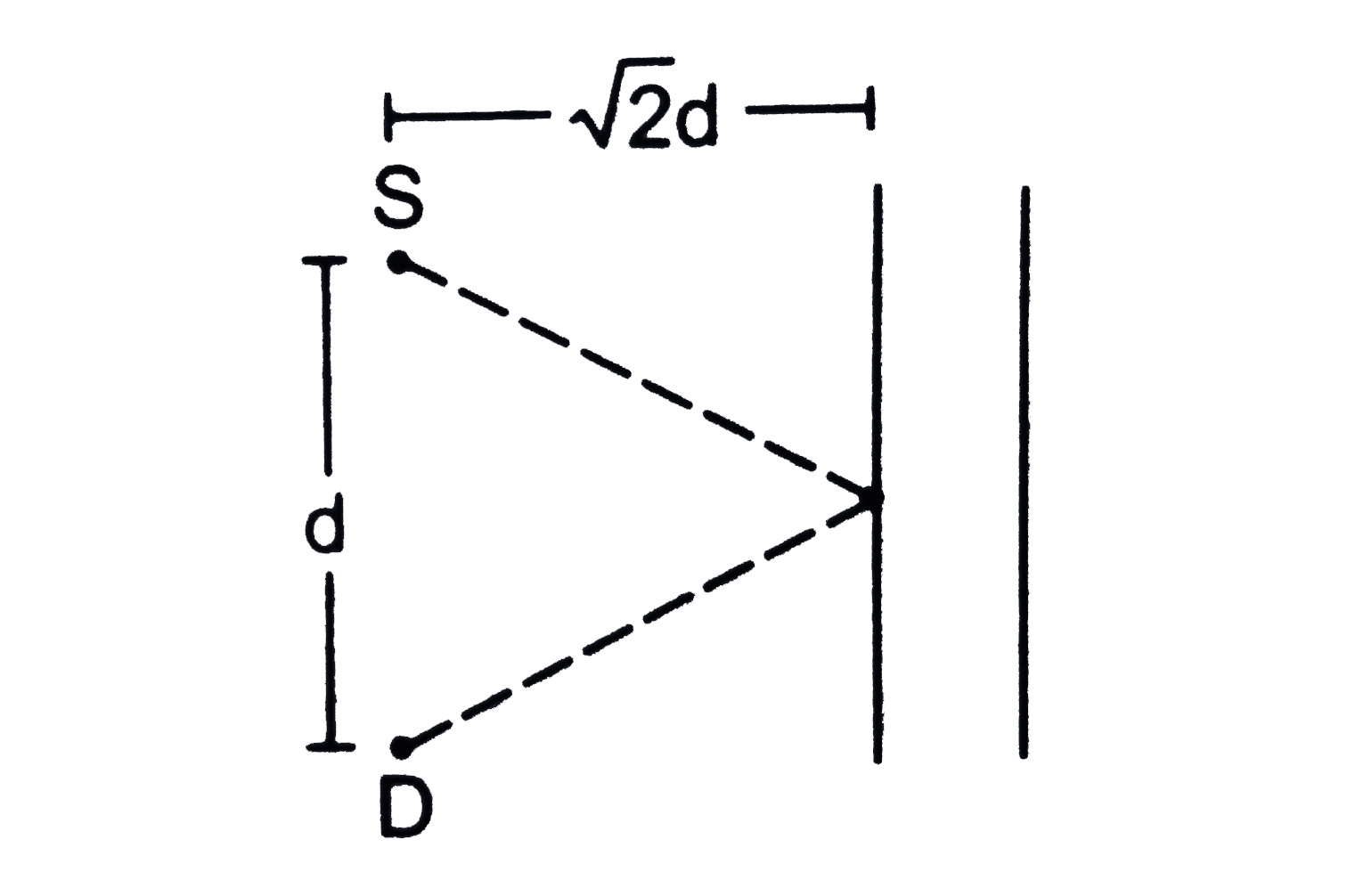
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View SolutionIn the Balmer series spectra of hydrogen , there is a line corresponding to wavelength 4344Å Calculate the number of highest orbits from electron drops to greater other lines (R×c=3.289×1015)
View SolutionAn aeroplane is flying horizontally at a height of 23km with a velocity of 15 km/h. Find the rate at which it is receding from a fixed point on the ground which it passed over 2 min ago.
View SolutionAn aeroplane is flying horizontally at a height of 23km with a velocity of 15 km/h. Find the rate at which it is receding from a fixed point on the ground which it passed over 2 min ago.
View Solution
