Three charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
In the given equilateral triangle ABC of sides of length l, if we draw a perpedicular AD to the side BC.
AD=ACcos30∘=(√3/2) and the distance AO of the entroid O from A is (2/3) AD= (1/√3)l. By symmartry AO=BO=CO.
ForceF1on Q due to the charge 1 q at A=34πε0Qql2along AO
ForceF2on Q due to the charge 1 q at B=34πε0Qql2along BO
ForceF3on Q due to the charge 1 q at C=34πε0Qql2along cO
The resultant of forcesF2andF3is=34πε0Qql2along OA, by the parallelogram law. Therefore, the total force on Q=34πε0Qql2(ˆr−ˆr)=0, where ˆr is the unit vector along OA.
It is clear also by symmetry that the three forces will sum to zero. Suppose that the resultant force was non-zero but in some direction. Consider what would happen if the system was rotated through 60° about O
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
Three charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View SolutionThree charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View Solution
Knowledge Check
Consider three charges q1,q2 and q3 each equal to q, at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?
A3Qq4πε0l2B2Qq4πε0l2CQq2πε0l2DzeroConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2DzeroThree masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Three equal masses 2m each are placed at the vertices an equilateral triangle PQR
(i) What is the force acting on a mass m placed at the centroid G of the triangle ?
(ii) What is the force on mass m if the mass at the vertex P is quadrupled ?
Take PG = QG = RG = 1m

View SolutionThree positive charges of equal magnitude q are placed at the vertics of and equilatral triangle of side l. How can the system of charges be palced in equilibrium?
View SolutionThree charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the center of the triangle.
a. Find the net force on charge q.
b. If Q=−q, will the charges at the corners move toward the center or fly away from it ?
c. For what value of Q at O will the charges remain stationary ?
d. In situation (c), how much work is done in removing the charges to infinity?
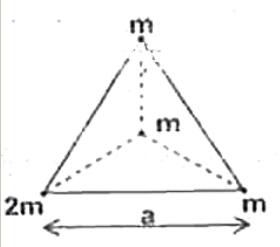
View SolutionThree point masses m,m and 2m are placed on the vertex of an equilateral triangle of side 'a' Another point mass 'm' is placed at the centroid of the triangle as shown in the figure. If the magnitude of net force on the point mass placed at centroid is KGm2a2 then find the value of K (G= universal gravitational constant )
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View Solution
