Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
The forces acting on charge q at A due to charges q at B and –q at C are F12 along BA and F13 along AC respectively, as shown in Fig. 1.10. By the parallelogram law, the total force F1 on the charge q at A is given by
F1 = F 1 ˆ r where 1 ˆ r is a unit vector along BC. The force of attraction or repulsion for each pair of charges has the
same magnitude F=q24πε0l2
Similarly the total force on charge −qatCisF3=√3Fˆn where ˆn is the unit vector along the direction bisecting the ∠BCA. It is interesting to see that the sum of the forces on the three charges is zero, i.e.,
F1+F2+F3=0
The result is not at all surprising. It follows straight from the fact that Coulomb’s law is consistent with Newton’s third law. The proof is left to you as an exercise
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
Three charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View SolutionThree charges of equal magnitude q is placed at the vertices of an equilateral triangle of side l. The force on a charge Q placed at the centroid of the triangle is
View Solution
Knowledge Check
Consider three charges q1,q2 and q3 each equal to q, at the vertices of an equilateral triangle of side l. What is the force on a charge Q placed at the centroid of the triangle?
A3Qq4πε0l2B2Qq4πε0l2CQq2πε0l2DzeroThree charges q1,q2,q3 each equal to q placed at the vertices of an equilateral triangle of side l . What will be the force on a charge Q placed at the centroid of triangle ?
A4NB5NC10NDZeroThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2
Consider three charges q1,q2 and q3 each equal to q at the vertices of an equilateral triangle of side 'l' what is the force on any charge due to remaining charges.
View SolutionConsider three charges q1,q2 and q3 each equal to q at the vertices of an equilateral triangle of side 'l' what is the force on any charge due to remaining charges.
View SolutionConsider three charges q1,q2 and q3 each equal to q at the verticles of an equilateral triangle of side 'l' what is the force on any charge due to remianing charges.
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.
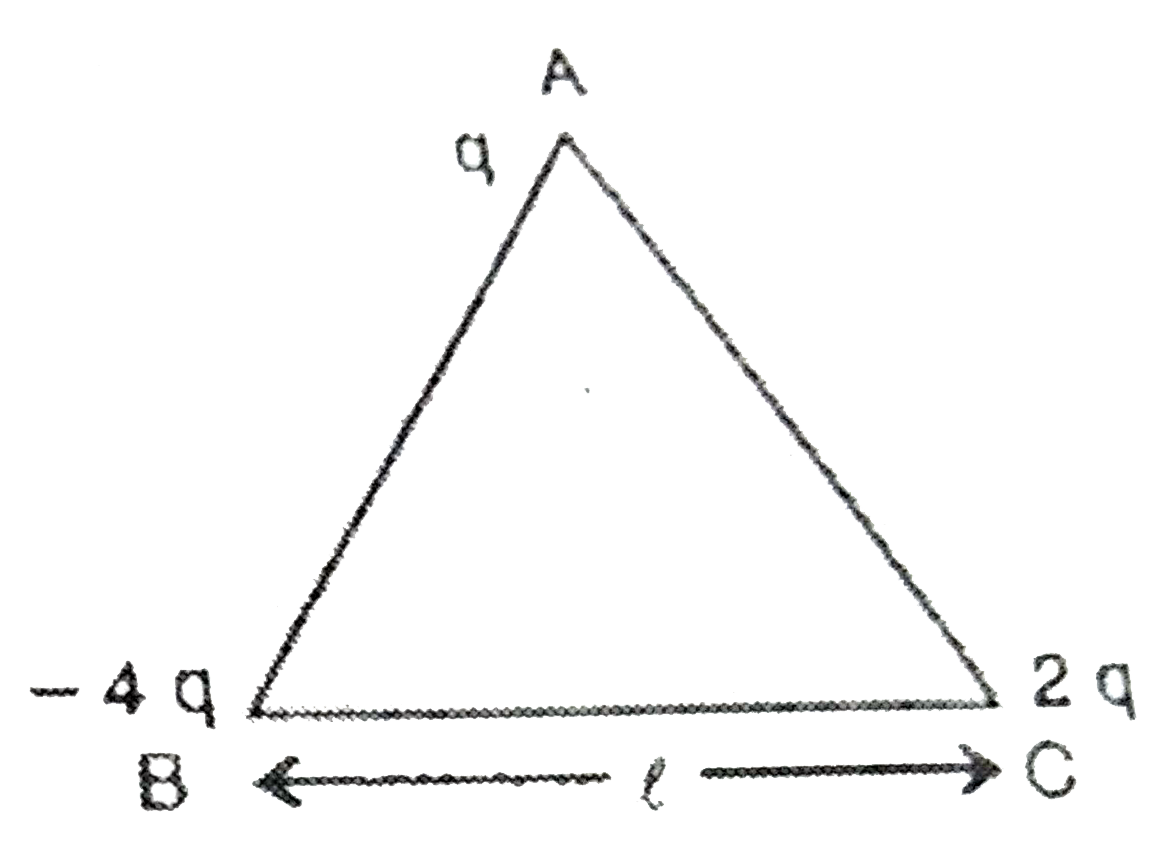
View Solution
