An object of mass 40 kg is raised to a height of 5 m above the ground. What is its potential energy ? If the object is allowed to fall, find its kinetic energy when it is half - way down.
The correct Answer is:2000 J, 1000 J
To solve the problem step by step, we will first calculate the potential energy of the object when it is raised to a height of 5 meters, and then we will determine its kinetic energy when it is halfway down.
Step 1: Calculate the Potential Energy (PE)
The formula for potential energy (PE) is given by:
PE=mgh
where:
- m = mass of the object (in kg)
- g = acceleration due to gravity (approximately 10m/s2)
- h = height above the ground (in meters)
Given:
- m=40kg
- g=10m/s2
- h=5m
Substituting the values into the formula:
PE=40kg×10m/s2×5m
PE=2000Joules
Step 2: Determine the Kinetic Energy (KE) when the object is halfway down
When the object is halfway down, it has fallen to a height of h2=52=2.5m.
Step 2.1: Calculate the Potential Energy at halfway down
Using the potential energy formula again:
PEhalf=mghhalf
where hhalf=2.5m:
PEhalf=40kg×10m/s2×2.5m
PEhalf=1000Joules
Step 2.2: Apply the Conservation of Energy Principle
According to the conservation of energy:
Initial Total Energy=Final Total Energy
This can be expressed as:
Initial KE+Initial PE=Final KE+Final PE
Initially, the object is at rest, so:
Initial KE=0
Thus:
0+2000J=KEfinal+1000J
Rearranging gives:
KEfinal=2000J−1000J
KEfinal=1000Joules
Final Answers:
1. The potential energy of the object when raised to a height of 5 m is 2000 Joules.
2. The kinetic energy of the object when it is halfway down is 1000 Joules.
PE=mgh
where:
- m = mass of the object (in kg)
- g = acceleration due to gravity (approximately 10m/s2)
- h = height above the ground (in meters)
- m=40kg
- g=10m/s2
- h=5m
PE=40kg×10m/s2×5m
PE=2000Joules
PEhalf=mghhalf
where hhalf=2.5m:
PEhalf=40kg×10m/s2×2.5m
PEhalf=1000Joules
Initial Total Energy=Final Total Energy
This can be expressed as:
Initial KE+Initial PE=Final KE+Final PE
Initially, the object is at rest, so:
Initial KE=0
Thus:
0+2000J=KEfinal+1000J
KEfinal=2000J−1000J
KEfinal=1000Joules
1. The potential energy of the object when raised to a height of 5 m is 2000 Joules.
2. The kinetic energy of the object when it is halfway down is 1000 Joules.
Topper's Solved these Questions
Similar Questions
A body of mass 5 kg is taken a height 5 m to 10 m .Find the increase in its potential energy (g=10 m s−2)
View SolutionAn object of mass 12 kg is at a certain height above the gorund if the potential energy of the object is 480J find the height at which the object is withj respect to the ground Given, g=10m/s2
View Solution
Knowledge Check
An object of mass 2 kg has linear momentum magnitude 6 kg⋅m/s. What is this object's kinetic energy?
A3JB6JC9JD12J
An object of mass 15kg is moving with a uniform velocity of 4m/s. what is the kinetic energy possessed by the object ?
View SolutionThe kinetic energy of an object of mass m moving with a velocity of 5 m//s is 25 J. What will be its kinetic energy when its velocity is doubled ? What will be its kinetic energy - when its velocity si increased three times ?
View SolutionA body of mass 0.2 kg falls from a height of 10 m to a height of 6 m above the ground. Find the loss in potential energy taking place in the body.
[g=10ms−2]
View SolutionA ball of mass 10 g falls from a height of y 5 m. It rebounds from the ground to a height of 4m. Find :
(a) the initial potential energy of the ball, (b) the kinetic energy of the ball just before the ground. striking the ground,
(c) the kinetic energy of the ball after striking the ground ,and
(d) the loss in kinetic energy on striking the ground .
Take g=9.8 m s−2.
View SolutionFind the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground.Given, g=9.8m/s2
View SolutionAn object of mass 'm' is allowed to fall freely from a point A as shown in the figure.
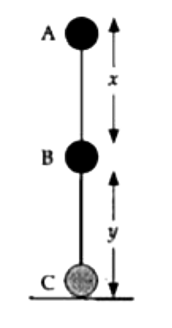
Calculate the total mechanical energy of object at:
Point A
View SolutionIf the mass of the object is more, its kinetic energy will be ......... (less/more)
View Solution
