Two points A and B move on the positive direction of x-axis and y-axis respectively, such that OA + OB K. Show that the locus of the foot of the perpendicular from the origin O on the line ABís (x + y)(x2 + y2) = Kxy. · (0,b)B Let the equation of AB be =1 a
Step by step video & image solution for Two points A and B move on the positive direction of x-axis and y-axis respectively, such that OA + OB K. Show that the locus of the foot of the perpendicular from the origin O on the line ABís (x + y)(x2 + y2) = Kxy. · (0,b)B Let the equation of AB be =1 a by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View SolutionA plane passes through a fixed point (a,b,c). Show that the locus of the foot of the perpendicular to it from the origin is the sphere x2+y2+z2−ax−by−cz=0.
View Solution
Knowledge Check
The foot of the perpendicular drawn from the origin on the line 3x+y=λ(λ≠0) is P. If the line meets x-axis at A and y-axis at B, then the ratio BP:PA is:
A9:1B1:3C3:1D1:9
A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
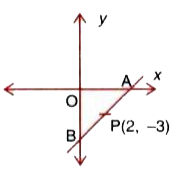
slope of line AB
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
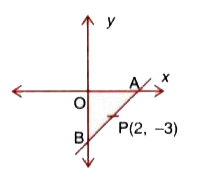
equation of line AB.
View SolutionA and B are any two points on the positive x and y axis respectively satisfying 2(OA)+3(OB)=10.1f P is the middle point of AB then the locus of P is-
View SolutionIf the line 3x-2y + 6=0 meets X-axis and Y-axis respectively at A and B, then find the equation of the circle with radius AB and centre at A.
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A,B moves on xandy axis respectively, then locus of mid point of AB is
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A, B moves on xandy axis respectively, then locus of mid point of AB is
View SolutionIf the first point of trisection of AB is (t,2t) and the ends A,B moves on xandy axis respectively, then locus of mid point of AB is
View Solution
