Rain is falling vertically with a velocity of 4 km hr−1 . A cyclist is going along a horizontal road with a velocity of 3 km hr−1 towards cast. Calculate the relative velocity of the rain with respect to the cyclist. In what direction must the cyclist hold his umbrella to save himself from the falling rain ? Solution in Telugu
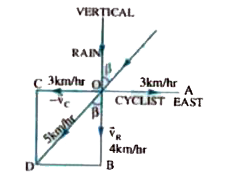
The situation is shown in Fig.
OA represents velocity →VCof cyclist, which is 3 km hr−1
OB represents velocity →CR of vertically falling rain, which is 4 km hr−1
OC represents −→vC opposite of velocity of the cyclist.
OD represents →VR+(−→vC)=→vR−→vC velocity of rain relative to cyclist.
In parallelogram OBDC,
OC=3kmhr−1OB=4kmhr−1
∠BOC=90∘
Hence OD=√(OC)2+(OB)2=√(3)2+(4)2=√9+16=√25=5kmhr−1
tanBη=BDOB=OCOB=34=0.75=tan36∘52.,i.eβ=36∘−52. east of vertical .
The cyclist must hold his umbrella at 36∘−52. with vertical in the direction of his motion (i.e. east).
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - LONG ANSWER TYPE QUESTIONS5videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS9videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)4videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)6videos
GEOMETRICAL OPTICS
Similar Questions
State parallelogram law of vectors . Derive an expression for the magnitude and direction of the resultant vector .
09:28View SolutionState and prove the parallelogram law of vectors.
02:21View SolutionFour identical point charges are fixed at the four corners of a square of a side length l. Another charged particle of mass m and charge +q is projected towards centre of square from a large, distance along the line perpendicular to plane of square. The minimum value of initial velocity V0 in m/s required to cross the square is? (m=1gm.l=4√2m,Q=1μc,q=0.5μc)
 01:16View Solution
01:16View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
05:40View SolutionA stationary person observes that rain is falling vertically down at 30 km h^-1 . A cyclist is moving up on an inclined plane making an angle 30^@ with horizontal at 10 km h^-1 . In which direction should the cyclist hold his umbrella to prevent himself from the rain ?
View SolutionRaindrops are falling vertically with a velocity 10m/s. To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of 20m/s. The velocity of cyclist is :-
06:57View SolutionRain is falling with a speed of 4nVs inadirection making an angle of 30^(@) with vertical towards south. What should be the magnitude & direction of velocity of cyclist to hold his umbrella exactly vertical, so that rain does not wet him:
02:19View SolutionA cyclist is moving due east with a velocity of 10 km h^(-1) . There is no wind and rain appoars to fall at an angle of 10^(@) to the vertical. Calculate the actual speed of the rain.
02:34View Solution(A): Rain is falling vertically downwards with velocity 6 km/hr. A man walks with a velocity of 8 km/hr. Relative velocity of rain w.r.t. the man is 10km/hr. (R): Relative velocity is the ratio of two velocities.
03:46View SolutionA stationary person observes that rain is falling vertically down at 30km/hr. A cyclist is moving up on an inclined plane making an angle 30∘ with horizontal at 10km/hr. In which direction should the cyclist hold his umbrella to prevent himself from the rain ?
01:15View SolutionRain droplets are falling in vertically downward direction with velocity 5 m //s . A cyclist is moving in northward direction with velocity 10 m/s. The rain droplets will appear to the cyclist to be coming from
View SolutionA man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
02:59View SolutionRain is falling vertically at 4 km *h^(-1) . What will be the apparent velocity and direction of the rain to a man moving horizontally at 3 km *h^(-1) ?
06:01View SolutionA cyclist acceleration from rest to a velocity of 72 km hr^(-1) in 10sec. If the cyclist is in straight track the acceleration of the cyclist is:
05:53View SolutionRain is falling vertically with a velocity of 4kmhr−1 . A cyclist is going along a horizontal road with a velocity of 3kmhr−1 towards east. Calculate the relative velocity of the rain with respect to the cyclist . In what direction must the cyclist hold his umbrella to save himself from the falling rain?
02:29View Solution

