Rain droplets are falling in vertically downward direction with velocity 5m/s. A cyclist is moving in northward direction with velocity 10 m/s. The rain droplets will appear to the cyclist to be coming from
tan−1(2) above south horizon
tan−1(12) above north horizon
Vertically downward
tan−1 (2) above north horizon
The correct Answer is:B
To solve the problem, we need to determine the direction from which the rain droplets appear to be coming to a cyclist moving northward while the rain is falling vertically downward. We can use vector addition to find the apparent direction of the rain relative to the cyclist.
1. Identify the velocities:
- The velocity of the rain droplets, Vr, is 5m/s downward.
- The velocity of the cyclist, Vc, is 10m/s northward.
2. Set up a coordinate system:
- Let the downward direction be negative y (i.e., −y).
- Let the northward direction be positive x (i.e., +x).
- Thus, the rain's velocity vector can be represented as →Vr=(0,−5) m/s.
- The cyclist's velocity vector can be represented as →Vc=(10,0) m/s.
3. Determine the relative velocity of the rain with respect to the cyclist:
- The relative velocity →Vrel is given by:
→Vrel=→Vr−→Vc=(0,−5)−(10,0)=(−10,−5)m/s
4. Calculate the angle of the apparent direction of the rain:
- The components of the relative velocity are Vrel,x=−10m/s (westward) and Vrel,y=−5m/s (downward).
- To find the angle θ that the rain appears to come from, we can use the tangent function:
tan(θ)=|Vrel,y||Vrel,x|=510=12
- Therefore,
θ=tan−1(12)
5. Determine the direction:
- The angle θ is measured from the negative x-axis (westward) towards the negative y-axis (downward).
- This means the rain appears to come from an angle θ above the horizontal line pointing north.
6. Final Answer:
- The rain droplets will appear to the cyclist to be coming from an angle θ=tan−1(12) above the northward direction.
- The velocity of the rain droplets, Vr, is 5m/s downward.
- The velocity of the cyclist, Vc, is 10m/s northward.
- Let the downward direction be negative y (i.e., −y).
- Let the northward direction be positive x (i.e., +x).
- Thus, the rain's velocity vector can be represented as →Vr=(0,−5) m/s.
- The cyclist's velocity vector can be represented as →Vc=(10,0) m/s.
- The relative velocity →Vrel is given by:
→Vrel=→Vr−→Vc=(0,−5)−(10,0)=(−10,−5)m/s
- The components of the relative velocity are Vrel,x=−10m/s (westward) and Vrel,y=−5m/s (downward).
- To find the angle θ that the rain appears to come from, we can use the tangent function:
tan(θ)=|Vrel,y||Vrel,x|=510=12
- Therefore,
θ=tan−1(12)
- The angle θ is measured from the negative x-axis (westward) towards the negative y-axis (downward).
- This means the rain appears to come from an angle θ above the horizontal line pointing north.
- The rain droplets will appear to the cyclist to be coming from an angle θ=tan−1(12) above the northward direction.
Similar Questions
Raindrops are falling vertically with a velocity 10m/s. To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of 20m/s. The velocity of cyclist is :-
View SolutionRain is falling vertically downward with velocity 4m/s. A man is moving horizontally with velocity 3m/s, the velocity of rain with respect to man is
View Solution
Knowledge Check
A particle moves in the direction of east for 2s with velocity of 15m/s .Then it moves towards north for 8s with a velocity of 5m/s . The average velocity of the particle is (in m/s)
A1 m/sB5 m/sC7 m/sD10 m/s
Rain is falling vertically downwards with a velocity of 2m//s. A person is runing to the North with a velocity of 2√3m/s. Find out the velocity and direction of rain as appeared to the person.
View SolutionA 150 m long train is moving in north direction with a velocity of 5m/s and a parrot is also moving in north direction with a velocity of 10 m/s, then find out (i) The time taken by parrot to cross the train (ii) Distance travel by the parrot during the crossing.
View SolutionAn object is falling vertically downwards with velocity 10m/s.In terms ofˆiandˆj find the image velocity. M

View SolutionRain is falling vertically with a velocity of 4 km hr−1 . A cyclist is going along a horizontal road with a velocity of 3 km hr−1 towards cast. Calculate the relative velocity of the rain with respect to the cyclist. In what direction must the cyclist hold his umbrella to save himself from the falling rain ?
View SolutionA stone is thrown in a vertically upward direction with a velocity of 5m/s. If the acceleration of the stone during its motion is 10m/s2 in the downward direction, what will be the height attained by the stone and how much time will take to reach there ?
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
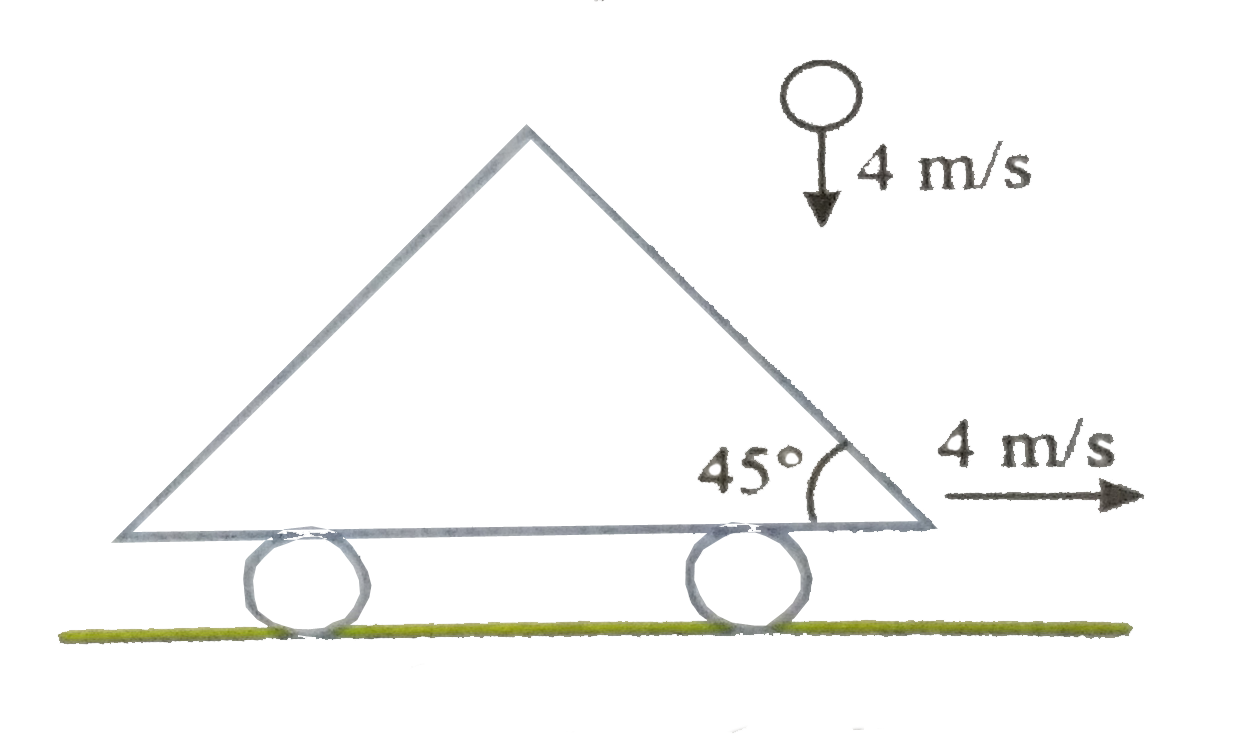
View SolutionA pebble thrown vertically upwards with an initial velocity 50 m s−1 comes to a stop in 5 s. Find the retardation.
View Solution
