When a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l/3 and 2l/3, and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure. Find the stretch in each of the spring.
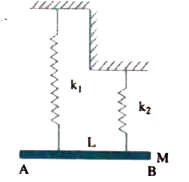 Solution in Telugu
Solution in Telugu
As it given that the mass M stretches the original spring by a distance x,
we have kx=Mg (or) k=Mgx......... (1)
The new force constants of the two springs can be given by using equations
k1=kegll1andk2=keqll2as,k1=3kandk2=3k2
Let we take the stretch in the two springs be x1andx2 we have for the equilibrium of the rod
k1x1+k2x2=Mg (or) 2kx1+3k2x2=Mg
From equation (1) , we have x1+x22=x3......... (2)
As the rod is horizontal and in static equilibrium , we have net torque acting on the rod about any point on it must be zero. Thus we have torquie on it above end A are
k2x2L=Mg(L)2
(or) x2=Mg2k2=Mg3k=x3
Using this value of x2 in equation (2) ,
we have x1=x6
This can also be directly obtained by using torque zero about point B on the rod as
k1x1L=Mg(L)2
(or) x1=Mg2k1=Mg6k=x6
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:LONG ANSWER TYPE QUESTIONS
Explore 4 Videos
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:SHORT ANSWER TYPE QUESTION
Explore 5 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 6 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 16 Videos
Similar Questions
State Newton's three laws of motion and derive the relation F= ma.
View SolutionState the Newton's laws of motion. What is the SI unit of force ?
View SolutionA fish is at a depth of 12 cm in water is viewed by an observer on the bank of a lake. To what height the image of the fish is raised in cm ?
View SolutionName the output function in the following circuit

View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
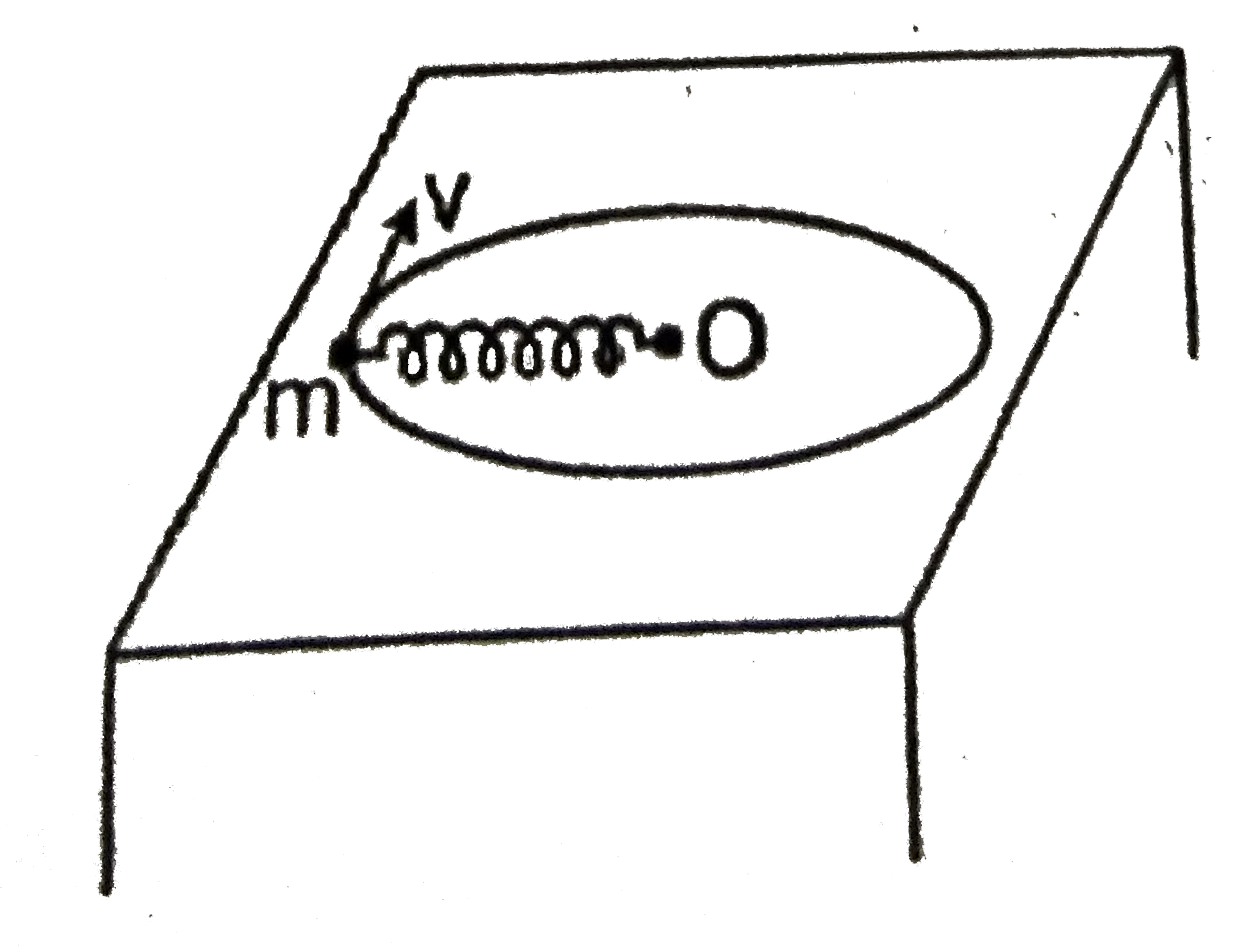
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionWhen a mass M is attached to the spring of force constant k , then the spring stretches by . If the mass oscillates with amplitude l , what will be maximum potential energy stored in the spring
View SolutionA horizontal metallic rod of mass m and length l is supported by two vertical identical springs of spring constant k each and natral length i_(0) A current l is flowing in the rod in the direction shown if the rod is in equilibrium then the length of each spring in this state is:
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of lengths l//3 and 2l//3 , and the two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure-2.111. Find the stretch in each of the spring.
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled a part symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is.
View Solutionस्प्रिंग नियतांक K की एक स्प्रिंग पर m द्रव्यमान लटकाया गया है। अब स्प्रिंग को दो बराबर भागों में काटकर किसी एक पर ही द्रव्यमान लटकाया जाता है , तो नया स्प्रिंग नियतांक होगा
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionWhen a mass M hangs from a spring of length l, it stretches the spring by a distance x. Now the spring is cut in two parts of length l//3"and" 2l//3 , and two springs thus formed are connected to a straight rod of mass M which is horizontal in the configuration shown in figure . Find the stretch in each of the spring
View Solution
