Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
12kx2
−12kx2
14kx2
−14kx2
The correct Answer is:D
To find the work done by the spring on each mass when two equal masses are attached to the ends of a spring and stretched symmetrically, we can follow these steps:
1. Understanding the System:
- We have two equal masses (let's call them m1 and m2) attached to a spring with spring constant k.
- The spring is stretched symmetrically by a length x from its natural length.
2. Work Done by the Spring:
- The work done by the spring when it is stretched is related to the potential energy stored in the spring.
- The potential energy U stored in a spring when stretched by a length x is given by:
U=12kx2
3. Work Done on Each Mass:
- Since the two masses are equal and the spring is stretched symmetrically, the work done by the spring on each mass will be half of the total potential energy stored in the spring.
- Therefore, the work done on each mass W is:
W=12(12kx2)=14kx2
4. Direction of Work Done:
- The work done by the spring on each mass is negative because the spring force acts in the opposite direction to the displacement of the masses. Thus:
W=−14kx2
Final Answer:
The work done by the spring on each mass is:
W=−14kx2
- We have two equal masses (let's call them m1 and m2) attached to a spring with spring constant k.
- The spring is stretched symmetrically by a length x from its natural length.
- The work done by the spring when it is stretched is related to the potential energy stored in the spring.
- The potential energy U stored in a spring when stretched by a length x is given by:
U=12kx2
- Since the two masses are equal and the spring is stretched symmetrically, the work done by the spring on each mass will be half of the total potential energy stored in the spring.
- Therefore, the work done on each mass W is:
W=12(12kx2)=14kx2
- The work done by the spring on each mass is negative because the spring force acts in the opposite direction to the displacement of the masses. Thus:
W=−14kx2
The work done by the spring on each mass is:
W=−14kx2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Objective -28videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Exercises64videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Worked out Examples14videos
WORK AND ENERGY
- BOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer7videos
WAVE MOTION AND WAVES ON A STRING
Similar Questions
Two equal masses are attached to the two end of a spring of force constant k the masses are pulled out symmetrically to stretch the spring by a length 2x0 over its natural length. Find the work done by the spring on each mass.
View SolutionWhen a 20 g mass hangs attached to one end of a light spring of length 10 cm, the spring stretches by 2 cm. The mass is pulled down until the total length of the spring is 14 cm. The elastic energy, (in Joule) stored in the spring is :
View Solutiona block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
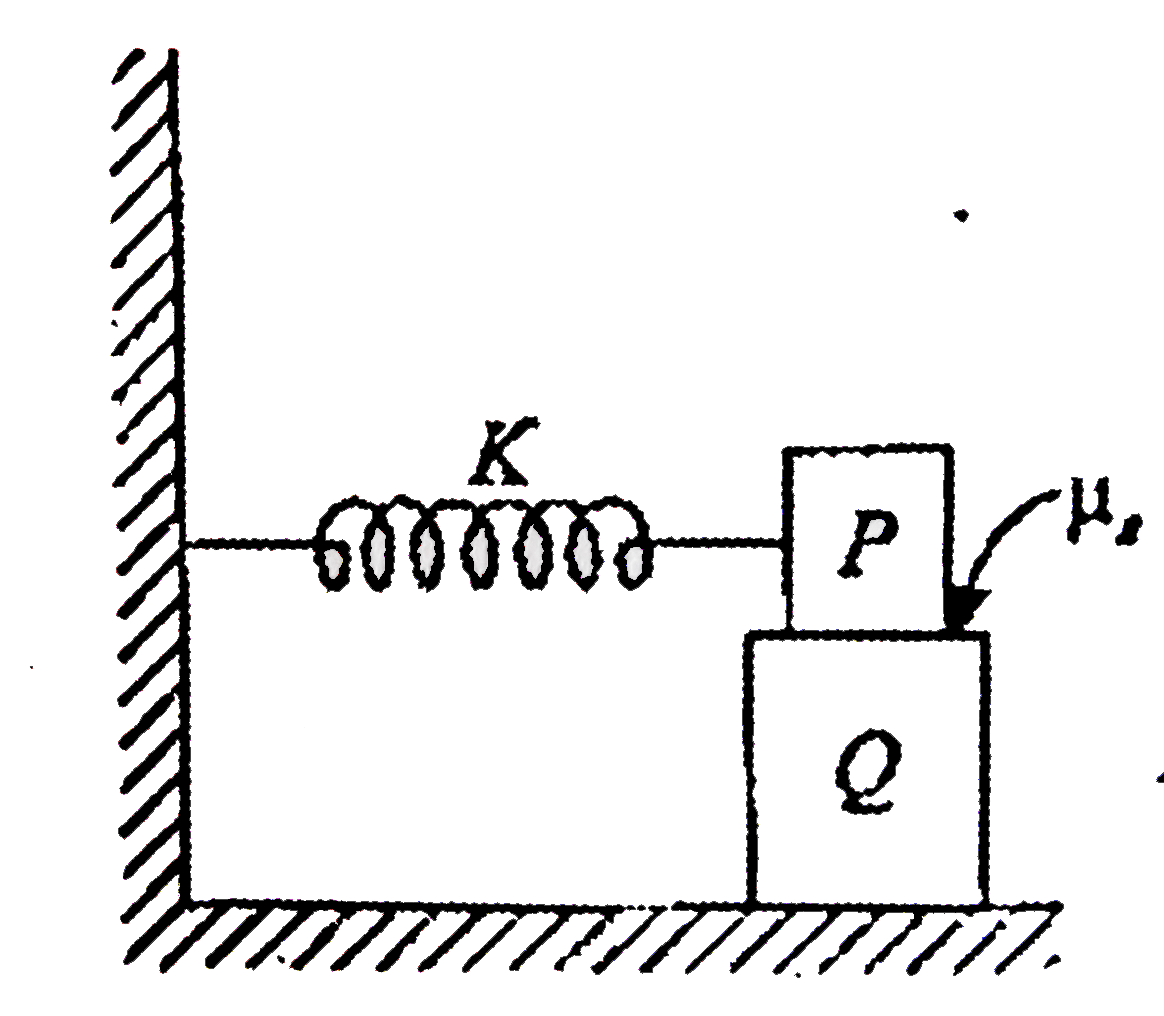 View Solution
View SolutionA spring of force constant K is first stretched by distance a from its natural length and then further by distance b. The work done in stretching the part b is
View SolutionBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)
 View Solution
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionAn elevatore is moving up with a constant velocity. Two different masses are attached to two different springs of same spring constant. Say you do two operations expanding the spring or compressing the spring by the same distance. Which operation consumes more energy: expanding the spring or compressing it?
View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length
 View Solution
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
View Solution

