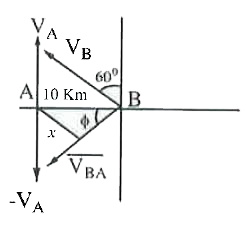
Ship A is 10km due west of ship B. Ship A is heading directly north ar a speed of 30 kmph while ship B is heading in a direction 600 west of north at a speed 20kmph. Their closest distance of approach will be....

Text Solution

Verified by Experts

$¯ ¯¯¯ ¯ V_{A} = 30 j ¯ ¯¯¯ ¯ V_{B} = 20 {sin 60}^{\circ} (i) + 20 Cos (60) (ˆ j)$
$= - 10 \sqrt{3 i} + 10 ˆ j$
$¯ ¯¯¯¯¯ ¯ V_{B A} = ¯ ¯¯¯ ¯ V_{A} = - 20 ˆ i - 10 \sqrt{3 i}$
If $ϕ$ is the angle made by $¯ ¯¯¯¯¯ ¯ V_{B A}$ with X axis
$Tan ϕ = \frac{20}{10 \sqrt{3}} = \frac{2}{\sqrt{3}} and sin ϕ = \frac{2}{\sqrt{7}}$
From $Δ A B C, \frac{x}{10} \times \frac{2}{\sqrt{7}}$
$x = \frac{20}{\sqrt{7}} = 7.6 K m$

Updated on:21/07/2023

A ship is travelling due north at 40 kmph. The captain of the finds that a second ship is always sailing $60^{\circ}$ west of north at a speed of 40 kmph. The velocity of the second ship then must be
A40 kmph, $30^{\circ}$ west of north
B40 kmph. $60^{\circ}$ west of south
C $40 \sqrt{3}$ kmph, $30^{\circ}$ west of north
D $40 \sqrt{3}$ kmph, $60^{\circ}$ west of south
A ship is travelling due east at a speed of $15 k m / h .$ Find the speed of a boat heading $30^{\circ}$ east of north if it appears always due north from the ship.
A $30 k m / h$
B $\frac{15 \sqrt{3}}{2} k m / h$
C $10 \sqrt{3} k m / h$
D $20 k m / h$
Ship A is located 4 km north and 3 km east of ship B. Ship A has a velocity of $20 k m h^{- 1}$ towards the south and ship B is moving at $40 k m h^{- 1}$ in a direction $37^{\circ}$ north of east. X and Y-axes are along east and north directions, respectively
AVelocity of A relative to B is $(- 32 ˆ i - 44 ˆ j) k m / h$
BPosition of A relative to B as a function of time is given by $r_{A B} = [(3 - 32 t) ˆ i + (4 - 44 t) ˆ j] k m$
CVelocity of A relative to B is $(32 ˆ i - 44 ˆ j) k \frac{m}{h}$
DPosition of A relative to B as a function of time is given by $(32 t ˆ i - 44 t ˆ j) k m$