Ship A is 10km due west of ship B. Ship A is heading directly north at a speed of 30 kmph while ship B is heading in a direction 60° west of north at a speed 20kmph. Their closest distance of approach will be........
To solve the problem of finding the closest distance of approach between Ship A and Ship B, we can follow these steps:
Step 1: Understand the Positions and Velocities
- Ship A is located 10 km due west of Ship B.
- Ship A is moving north at a speed of 30 km/h.
- Ship B is moving at a speed of 20 km/h in a direction 60° west of north.
Step 2: Set Up the Coordinate System
- Let’s place Ship B at the origin (0, 0).
- Therefore, Ship A will be at (-10, 0) in a Cartesian coordinate system, where the positive y-axis is north and the positive x-axis is east.
Step 3: Determine the Velocity Components
- Velocity of Ship A (V_A):
- Since Ship A is moving directly north, its velocity vector is:
VA=(0,30) km/h
- Velocity of Ship B (V_B):
- Ship B is moving 60° west of north. The components of its velocity can be calculated using trigonometry:
VB=(20sin(60°),20cos(60°))=(20⋅√32,20⋅12)=(10√3,10) km/h
Step 4: Calculate the Relative Velocity
- The relative velocity of Ship B with respect to Ship A (V_BA) is given by:
VBA=VB−VA=(10√3,10)−(0,30)=(10√3,−20) km/h
Step 5: Calculate the Magnitude of the Relative Velocity
- The magnitude of the relative velocity can be calculated using the Pythagorean theorem:
|VBA|=√(10√3)2+(−20)2=√300+400=√700=10√7 km/h
Step 6: Determine the Time of Closest Approach
- The closest distance occurs when the rate of change of distance between the two ships is zero. The distance between the two ships can be expressed as a function of time, and we can find the time at which this distance is minimized.
- The distance function D can be expressed as:
D(t)=√(10+10√3t)2+(30−20t)2
- To find the time of closest approach, we differentiate D with respect to t and set the derivative to zero.
Step 7: Solve for Time
- After differentiating and solving, we find:
t=√37 hours
Step 8: Calculate the Minimum Distance
- Substitute the value of t back into the distance formula to find the minimum distance:
Dmin=20⋅√37=20√37≈7.56 km
Final Answer
The closest distance of approach between Ship A and Ship B is approximately 7.56 km.
---
- Ship A is located 10 km due west of Ship B.
- Ship A is moving north at a speed of 30 km/h.
- Ship B is moving at a speed of 20 km/h in a direction 60° west of north.
- Let’s place Ship B at the origin (0, 0).
- Therefore, Ship A will be at (-10, 0) in a Cartesian coordinate system, where the positive y-axis is north and the positive x-axis is east.
- Velocity of Ship A (V_A):
- Since Ship A is moving directly north, its velocity vector is:
VA=(0,30) km/h
- Ship B is moving 60° west of north. The components of its velocity can be calculated using trigonometry:
VB=(20sin(60°),20cos(60°))=(20⋅√32,20⋅12)=(10√3,10) km/h
- The relative velocity of Ship B with respect to Ship A (V_BA) is given by:
VBA=VB−VA=(10√3,10)−(0,30)=(10√3,−20) km/h
- The magnitude of the relative velocity can be calculated using the Pythagorean theorem:
|VBA|=√(10√3)2+(−20)2=√300+400=√700=10√7 km/h
- The closest distance occurs when the rate of change of distance between the two ships is zero. The distance between the two ships can be expressed as a function of time, and we can find the time at which this distance is minimized.
- The distance function D can be expressed as:
D(t)=√(10+10√3t)2+(30−20t)2
- To find the time of closest approach, we differentiate D with respect to t and set the derivative to zero.
- After differentiating and solving, we find:
t=√37 hours
- Substitute the value of t back into the distance formula to find the minimum distance:
Dmin=20⋅√37=20√37≈7.56 km
The closest distance of approach between Ship A and Ship B is approximately 7.56 km.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS6videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS10videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
Similar Questions
A Ship A steams down north at a speed of 8 kmph. and ship B due west at a speed of 6 kmph. The velocity of A w.r.t. B is.
View SolutionShip A is located 4 km north and 3 km east of ship B. Ship A has a velocity of 20kmh−1 towards the south and ship B is moving at 40kmh−1 in a direction 37∘ north of east. X and Y-axes are along east and north directions, respectively
View SolutionA ship is travelling due east at a speed of 15km/h. Find the speed of a boat heading 30∘ east of north if it appears always due north from the ship.
View SolutionFrom a light-house an observer two ships A and B. Ship A proceeding towards north at a speed 20√2 km//h and ship B proceeding towards north-east at a speed of 20 km//h. Find in which direction and at what speed the ship B would appear to move to an observer standing on the deck of the ship A.
View SolutionTwo ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
View SolutionTwo ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
View SolutionAn aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The air-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go from A to B.
View SolutionShip A is travelling with a velocity of 5kmh−1 due east. A second ship is heading 30∘ east of north. What should be the speed of second ship if it is to remain always due north with respect to the first ship ?
View SolutionA ship A is moving Westwards with a speed of 10kmh−1 and a ship B 100km South of A is moving northwards with a speed of 10kmh−1. The time after which the distance between them shortest is
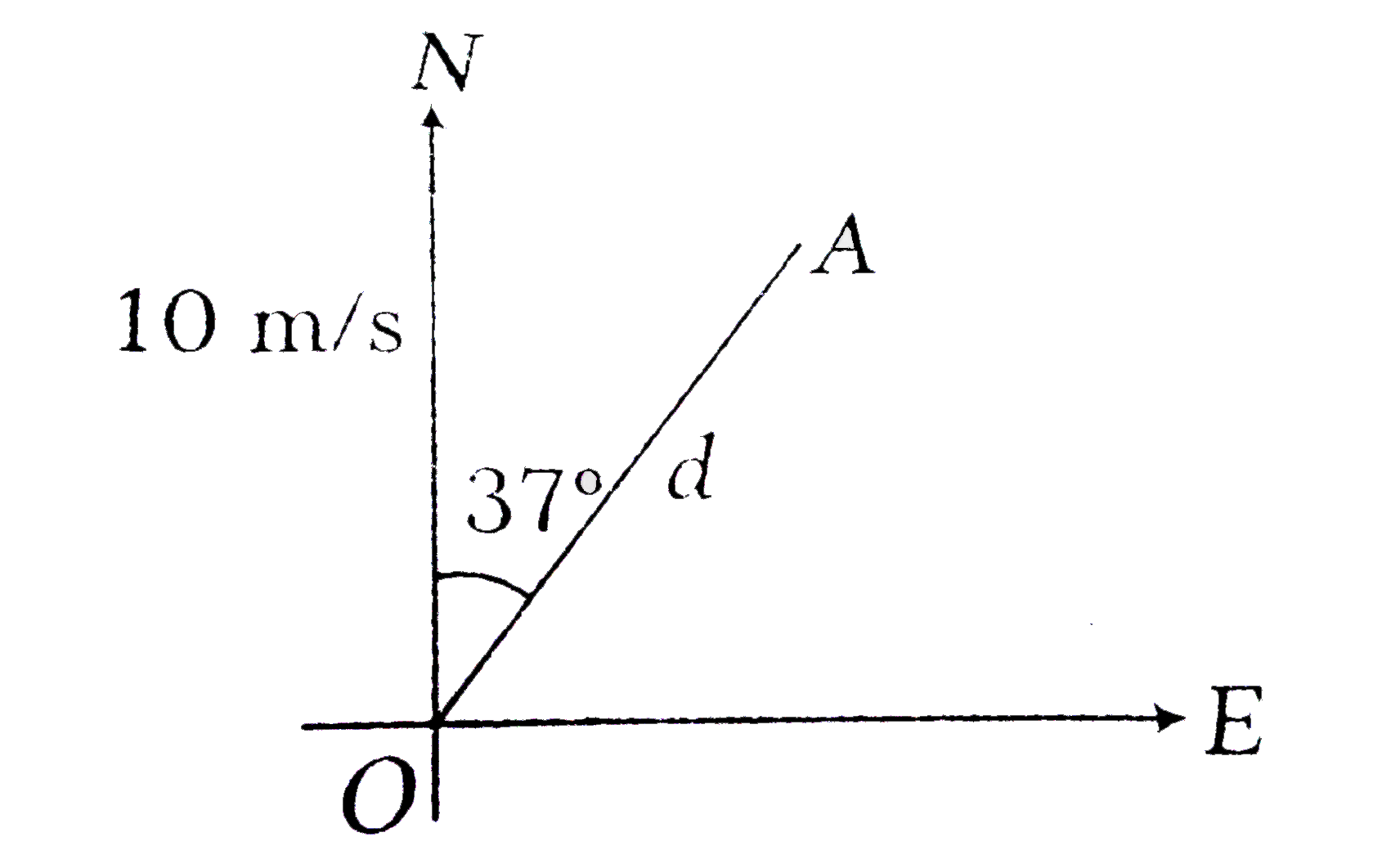
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
 View Solution
View Solution

