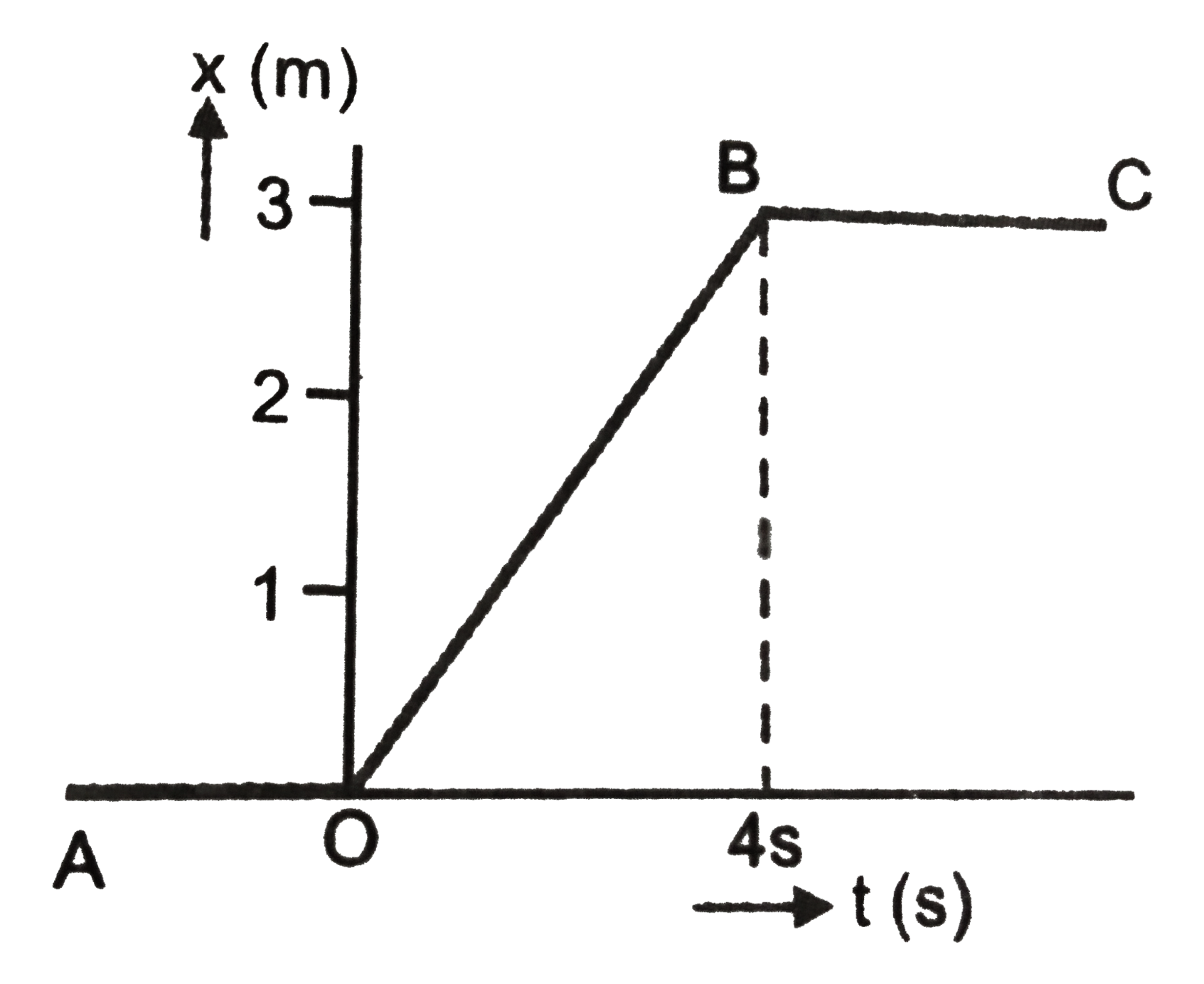
Figure shows the position-time graph of a particle of mass 4 kg, then
a) force on the particle for t<0,t>4s,0<t<4s? ?
b) impulse at t = 0 and t = 4 s. (consider one-dimensional motion only)

i) For t<0 in the position time graph is at O which means displacement of the particle is zero. i.e. particle is at rest at the origin. Hence force on the particle must be zero
ii) For 0 < t < 4 s, the position time graph OA has a constant slope. Therefore velocity of the particle is constant in this interval i.e. particle has zero acceleration. Hence force on the particle must be zero.
iii) For t > 4 s, the position time graph AB is parallel to time axis. Therefore, the particle remains at a distance 3m from the origin, i.e. it is at rest. Hence force on the particle is zero.
b) i) impulse at t = 0
We know, Impulse = change in linear momentum, Before t = 0 particle is at rest i.e. u = 0.
After t = 0, particle has a constant velocity
v=34=0.75m/s
∴ Impulse =m(v−u)=m(0.75−0)=3 kgm//s
(ii) ∴ Impulse at t = 4 s, Before t = 4s,
particle has a constant velocity u = 0.75 m/s After t = 4s, particle is at rest i.e. v = 0 Impulse = m(v−u)=4(0−0.75−−3 kg m/s
Similar Questions
Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View SolutionShown the position time graph of a particle of mass 4 kg What is the force on the particle for t<0,0<t<4s motion only
 .
.
View Solution
Knowledge Check
Figure shows the position time graph of a particle of mass 5kg. The force acting on the particle for 0<t<4s and 8s<t<12s respectively are,
 A5N,5NB5N.7.5NC5N,10ND0N,0N
A5N,5NB5N.7.5NC5N,10ND0N,0NFigure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
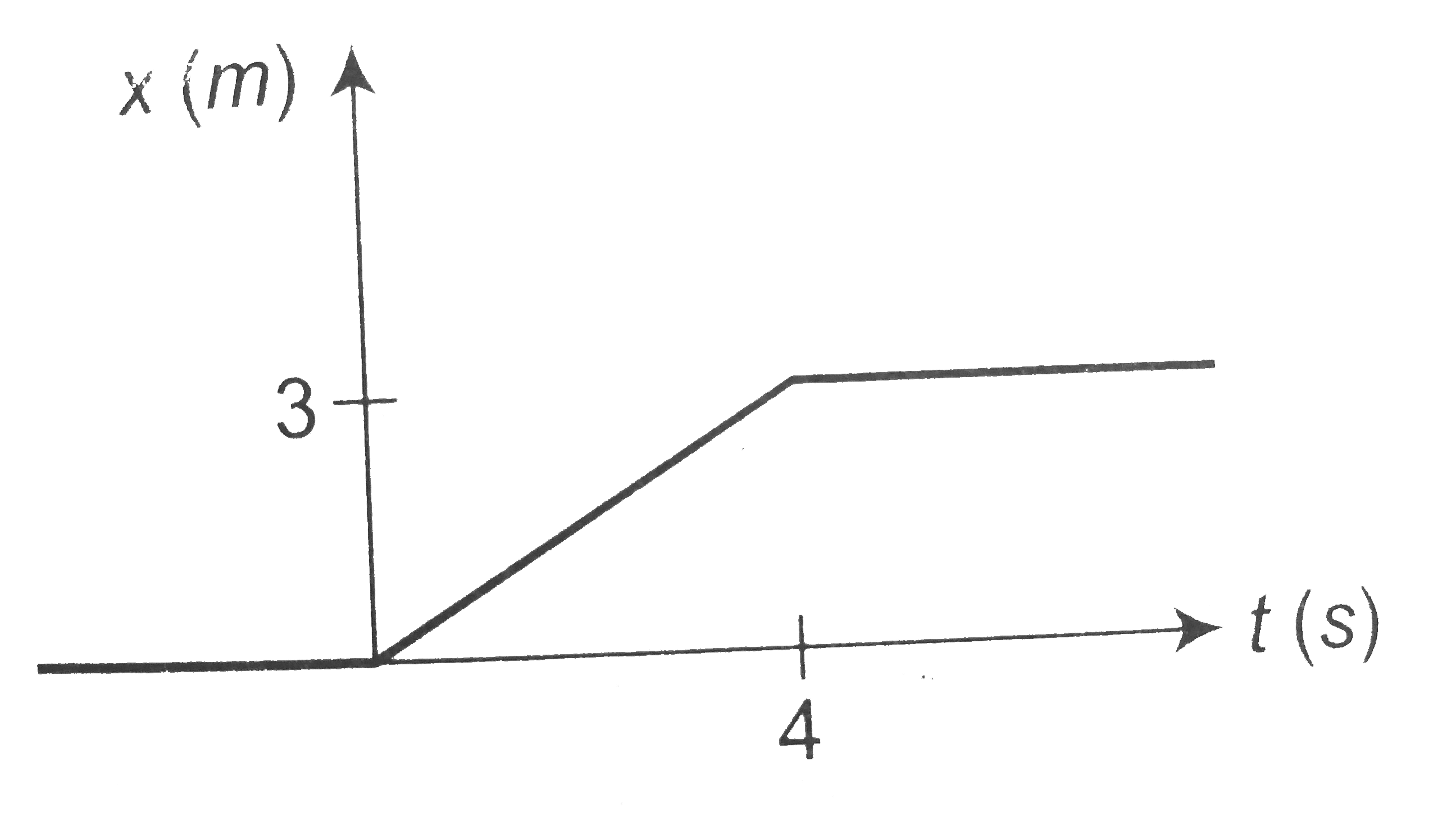 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3Figure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
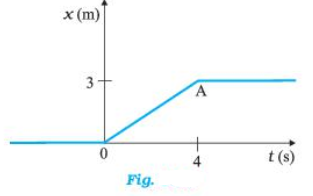
View SolutionFig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View SolutionThe position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :

View Solution
