12 सेमी त्रिज्या वाले एक वृत के अन्तर्गत खींचे जा सकने वाले सबसे बड़े वर्ग का क्षेत्रफल है -
24 सेमी 2
249 सेमी 2
288सेमी 2
196√2सेमी 2
The correct Answer is:C
Step by step video, text & image solution for 12 सेमी त्रिज्या वाले एक वृत के अन्तर्गत खींचे जा सकने वाले सबसे बड़े वर्ग का क्षेत्रफल है - by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- व्रतों से सम्बन्धित क्षेत्रफल BOOK - UP BOARD PREVIOUS YEARCHAPTER - व्रतों से सम्बन्धित क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न
3 Videos
- व्रतों से सम्बन्धित क्षेत्रफल BOOK - UP BOARD PREVIOUS YEARCHAPTER - व्रतों से सम्बन्धित क्षेत्रफल EXERCISE - लघु उत्तरीय प्रश्न
6 Videos
- वृत्त BOOK - UP BOARD PREVIOUS YEARCHAPTER - वृत्त EXERCISE - दीर्घ उत्तरीय प्रश्र
3 Videos
- समान्तर श्रेणियाँBOOK - UP BOARD PREVIOUS YEARCHAPTER - समान्तर श्रेणियाँEXERCISE - दीर्घ उत्तरीय प्रश्न
3 Videos
Similar Questions
एक घडी की मिनट की सुई जिसकी लम्बाई 14 सेमी है । इस द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए ।
View Solutionनिन्न आकृति में ABCD एक आयत है जो एक वृत के अन्तर्गन खींचा गया है यदि AB =8 सेमी और BC =6 सेमी , तो वृत्त का वह क्षेत्रफल ज्ञात कीजिए जो आयत के बाहर हैं ।π=3.14 का प्रयोग कीजिए ]

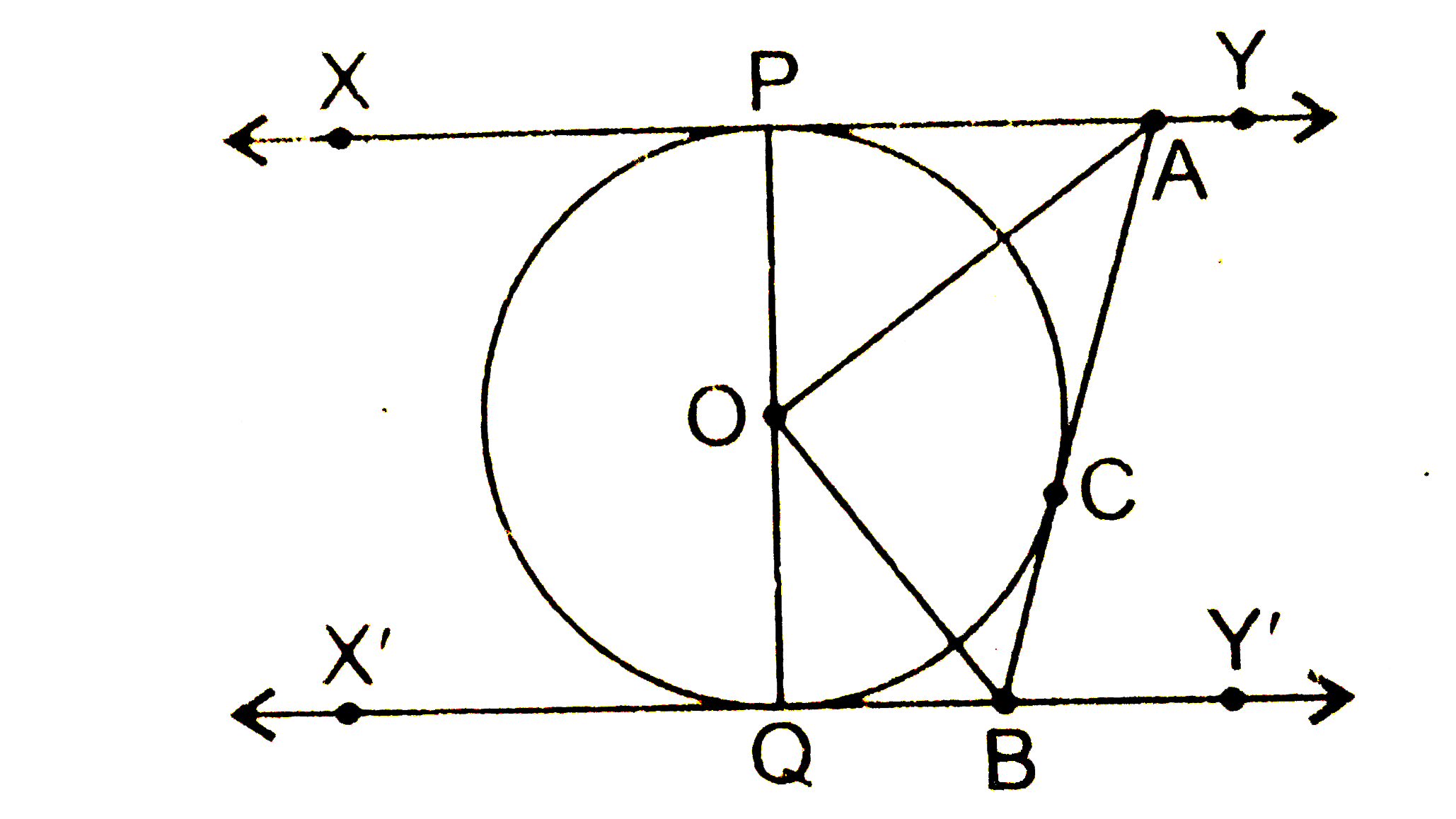
View Solutionआकृति में XY तथा X'Y', O केन्द्र वाले किसी वृत पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X'Y' को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ∠AOB=90∘ है ।
View Solution636 योगफल प्राप्त करने के लिए श्रेणी 9,17,25,…. के कितने पद लेने चाहिए ?
View Solutionदो चरों के रैखिक समीकरणो के युग्म में बदले जा सकने वाले समीकरण || उदाहरण
View Solutionदो चरों के रैखिक समीकरणों के युग्म में बदले जा सकने वाले समीकरण - भाग 01
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionदो चरो के रेखिक समीकरणों के युग्म मे बदले जा सकने वाले समीकरण |अभ्यास कार्य |सारांश
View Solutionदो चरो के रेखिक समीकरणों के युग्म मे बदले जा सकने वाले समीकरण |अभ्यास कार्य |सारांश
View Solutionदो चरों के रेखिक समीकरणो के युग्म मे बदले जा सकने वाले समीकरण |NCERT प्रश्नावली |सारांश
View Solutionदो चरों के रेखिक समीकरणो के युग्म मे बदले जा सकने वाले समीकरण |NCERT प्रश्नावली |सारांश
View SolutionAn equilateral triangle of side 12 cm is drawn. What is the area (in cm^2 ) of the largest square which can be drawn inside it? 12 सेमी. भुजा वाला एक समबाहु त्रिभुज बनाया गया। इसमें बनाए जा सकने वाले बडे वर्ग को क्षेत्रफल (सेमी. में) क्या है?
View SolutionThe in-radius of a triangle is 6 cm, and the sum of the length of its sides is 50cm. The area of the triangle (in sq. cm) is एक त्रिभुज को अंतः त्रिज्या 6 सेमी है, तथा इसके भुजाओं के लंबाई का योग 50 सेमी है। त्रिभुज का क्षेत्रफल (वर्ग सेमी में) ज्ञात करें।
View SolutionThe side of a square is 6 cm. Find the area of the largest circle that can be drawn inside the square. (π=227)
एक वर्ग की भुजा 6 cm है | वर्ग के अंदर बनने वाले सबसे बड़े वृत्त का क्षेत्रफल कितना है?
View SolutionWhat is the area of the largest square which can be inscribed in a circle of radius 14 cm? (π=227)
उस सबसे बड़े वर्ग का क्षेत्रफल ज्ञात करें जिसे 14 सेमी त्रिज्या वाले वृत्त के भीतर खींचा जा सकता है |
View SolutionWhat is the area of the largest square which can be inscribed in a circle of radius 28 cm?
उस सबसे बड़े वर्ग का क्षेत्रफल ज्ञात करें जिसे 28 सेमी त्रिज्या वाले वृत्त के भीतर खींचा जा सकता है |
View Solution
