A solid cylinder of mass m and radius R rest on a plank of mass 2m lying on a smooth horizontal surface. String connecting cylinder to the plank is passing over a massless pulley mounted on a movable light block B and the friction between the cylinder and the plank is sufficient to prevent slipping. if the block B is pulled with a constant forceF, the acceleration of the plank is 2Fxm then calculate x.

For the cylinder, F2−f=ma1 (1)
Taking moment of forces about C
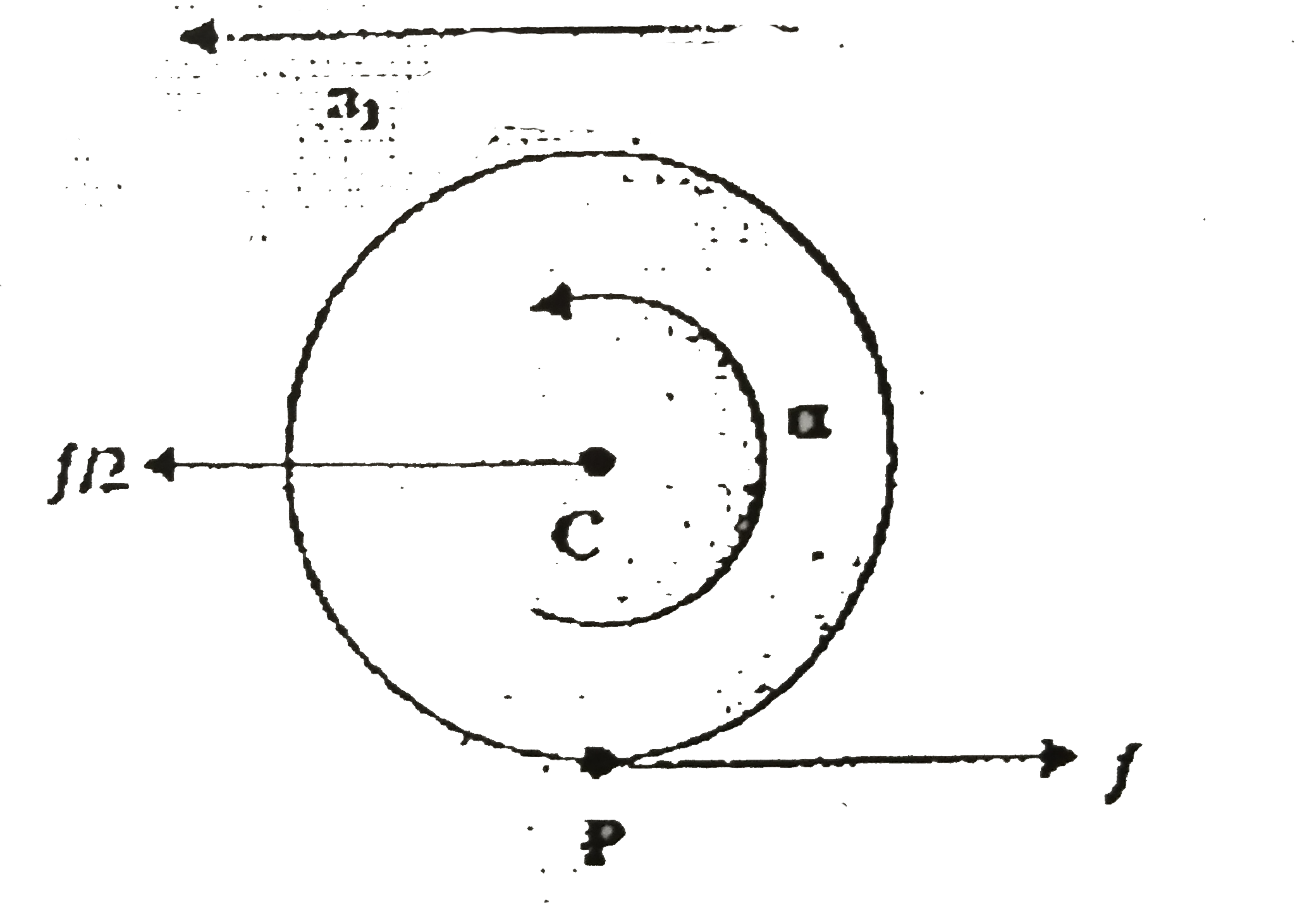
fR=la
⇒f=mRα2 (2)
∵1=mR2/2
for the plank, F2+f=(2m)a2 (3)
And at the point of contact P, the acceleration of the two bodies must be same

a1−Rα=a2 (4)
From 1 and 3, 2 and 4
F=(ma1+2ma2) and
F2+mRα2=2ma2
Subsitituting value of α and solving for a1 and a2 gives,
Accelecration of plank a2=2F7m
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank isView Solution
Knowledge Check
- Question 1 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Acceleration of the plank isA3F16mB11F8mC9F4mDZero - Question 2 - Select One
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2m - Question 3 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank isAF8B3F8C5F8D7F8
Find the acceleration of a system consisting of a cylinder of mass m and radius R and a plank of mass M placed an a smooth surface if it is pulled with a force F as shown Fig. Given that sufficient friction is present between the cylinder and the plank surface to prevent sliding of the cylinder.
 View Solution
View Solution
Find the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:
 View Solution
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isView SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
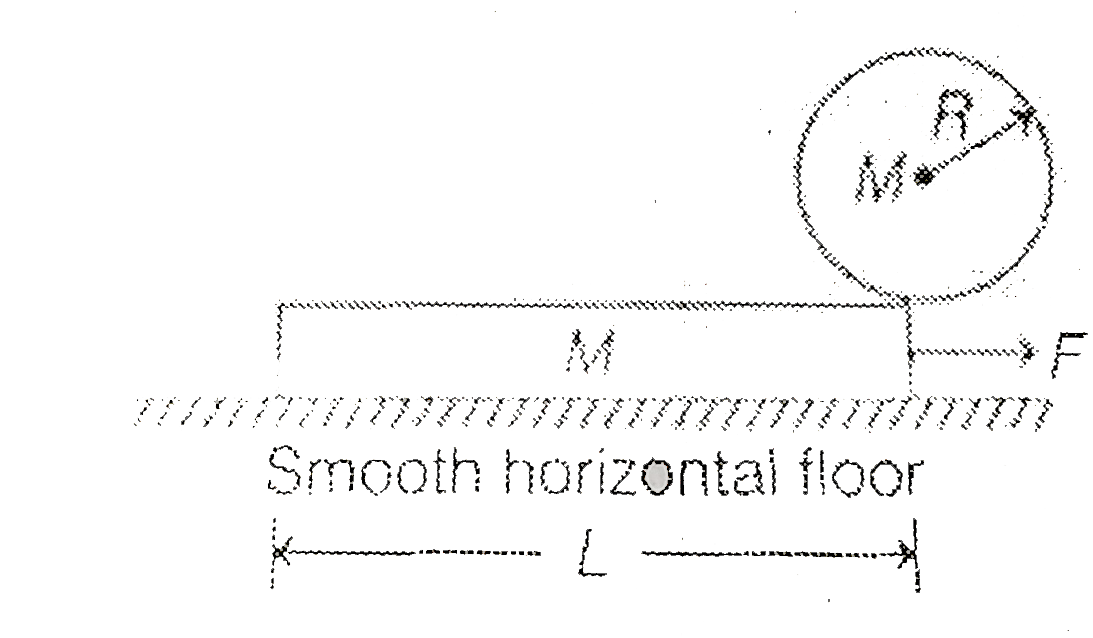
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of acceleration of plank isView Solution

