सीधी कोरों से बने एक लूप में A(0, 0, 0), B(L, 0, 0), C(L, L, 0), D(0, L, 0), E(0, L, L), F(0, 0, L) पर छह कोने हैं। एक चुम्बकीय क्षेत्र →B=B0(ˆi+ˆk)T क्षेत्र में उपस्थित है। लूप ABCDEFA (उसी क्रम में) से गुजरने वाला फ्लक्स होगा-
B0L2Wb
2B0L2Wb
√2B0L2Wb
4B0L2Wb
The correct Answer is:B
यहाँ, →B=B0(ˆi+ˆk)T

ABCD का सदिश क्षेत्रफल = L2ˆk
DEFA का सदिश क्षेत्रफल =L2ˆi
कुल सदिश क्षेत्रफल, →A=L2(ˆi+ˆk)
कुल चुम्बकीय फ्लक्स, ϕ=→B.→A=B0(ˆi+ˆk).L2(ˆi+ˆk)
=B0L2(1+1)=2B0L2 Wb
Topper's Solved these Questions
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- विद्युतचुम्बकीय प्रेरणBOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युतचुम्बकीय प्रेरणEXERCISE - बहुविकल्प प्रश्न पिटारा (प्रत्यावर्ती धारा जनित्र )
2 Videos
- विद्युत धारा BOOK - NCERT FINGERTIPS HINDICHAPTER - विद्युत धारा EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- विधुतचुम्बकीय तरंगे BOOK - NCERT FINGERTIPS HINDICHAPTER - विधुतचुम्बकीय तरंगे EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
अभिकथनः जब किसी कुंडली में धारा परिवर्तित होती है, तो यह समान कुंडली में वापस वि.वा.बल उत्पन्न करती है।
तर्कः वि.वा.बल किसी कुंडली में से गुजरने वाली धारा के विरुद्ध जड़त्व का माप है।
View Solutionएक लड़का किसी स्थिर साइकिल में पैडल मारता है, साइकिल के पैडल 0.10 m2 क्षेत्रफल वाली 200 फेरों की कुंडली से जुड़े हुए हैं। कुंडली प्रति सेकण्ड आधा चक्र (Revolution) घूर्णन कर लेती है तथा इसे कुंडली के घूर्णन अक्ष के लंबवत् 0.02 T के एकसमान चुम्बकीय क्षेत्र में रखा गया है। कुंडली में उत्पन्न अधिकतम वोल्टेज होगा-
View Solutionअभिकथन: विद्युत वाहक बल एक ऐसा बल होता है जो इलेक्ट्रॉन के प्रवाह एवं धारा उत्पन्न करने में मदद करता है।
तर्कः विद्युत वाहक बल सेल में वोल्टता पर निर्भर नहीं करता है।
View Solutionअभिकथनः विभिन्न प्रकार की विद्युतचुम्बकीय तरंगों के बीच मुख्य अन्तर उनकी तरंगदैर्घ्य या आवृत्तियों में होता है।
तर्क: विद्युतचुम्बकीय तरंगें समान चाल से निर्वात में गति करती हैं।
View SolutionA loop made of straight edegs has six corners at A(0,0,0), B(L, O,0) C(L,L,0), D(0,L,0) E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionMatch the following: {:(," ""Column-I",," ""Column-II"),((a),F = A sin(B t) + (1)/(C ln (Dx)) "For above equation to be dimensionally correct",(p),[A] = [M^(1)L^(1)T^(-1)]","[B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(0)L^(0)T^(-1)]),((b) ,"Pressure" = P + (1)/(2)rhov^(2) + gX ,(q),[A] = [M^(0)L^(1)T^(-1)]"," [B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(0)L^(0)T^(-1)]","),((c),X = At+(v)/(B ln(Cr)),(r),[A] = [M^(1)L^(1)T^(-2)]","[B] = [M^(0)L^(0)T^(-1)]","[C] = [M^(-1)L^(0)T^(1)]),(,,(s),"Dimensionally incorrect""):} (Where F = force, P = pressure, rho = density, t = time, v = velocity, a = acceleration, X = displacement)
View Solutionकारण देते हुए, बताइए की निम्नलिखित क्वांटम संख्या के कौन से मान संभव नहीं है-
(क) n=0,l=0,ml=0,ms=+1/2
(ख) n=1,l=0,ml=0,ms=−1/2
(ग) n=1,l=1,ml=0,ms=+1/2
(घ) n=2,l=1,ml=0,ms=−1/2
(ड) n=3,l=3,ml=−3,ms=+1/2
(च) n=3,l=1,ml=0,ms=+1/2
View SolutionExplain, giving reasons, which of the following sets of quantum numbers are not possible. (a) n=0, l=0, m_(1)=0, m_(s)= +1//2 (b) n=1, l=0, m_(l)=0, m_(s)=-1//2 (c) n=1, l=1, m_(l)=-0, m_(s)=+1//2 (d) n=2, l=1, m_(l)=0, m_(s)=-1//2 (e) n=3, l=3, m_(l)=-3, m_(s)=+1//2(f) n=3, l=1, m_(l)=0, m_(s)=+1//2
View SolutionA loop, made of straight edges has six corners at A(0,0,0), B(L,0,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field →B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is:
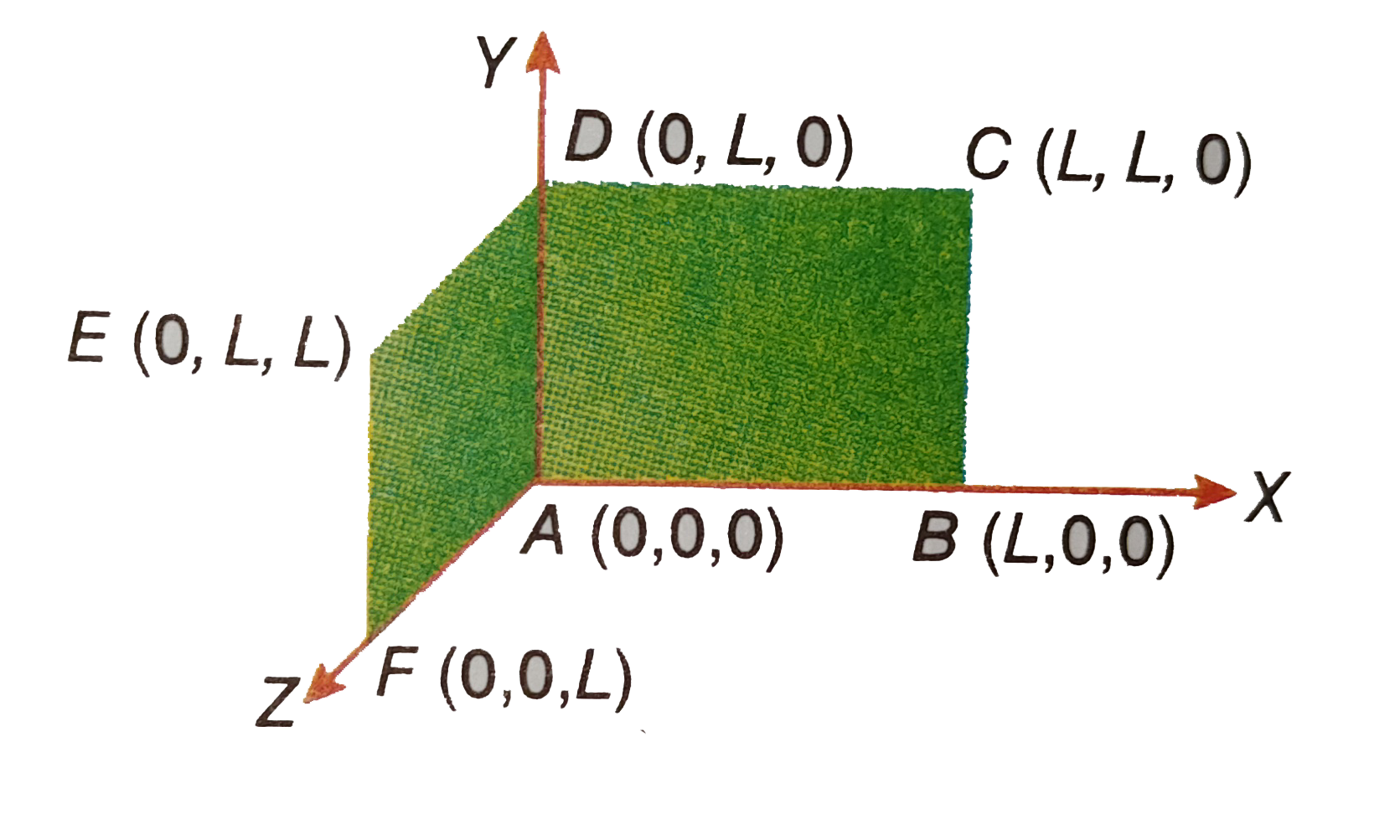
View SolutionExplain giving reasons , which of the following sets of quantum numbers are not possible .
a) n=0,l=0,ml=0,ms=+12
b) n=1,l=0,ml=0,ms=−12
c) n=1,l=1,ml=0,ms=+12
d) n=2,l=1,ml=0,ms=+12
e) n=3,l=3,ml=−3,ms=+12
f) n=3,l=1,ml=0,ms=+12
View SolutionAssertion :- Voltage across L (see figure) at t=0 is E Reason:- Because E=V_(L)+V_(R) and at t=0, i=0
View Solutionएक लूप सीधी भुजाओं से बना है, जिसमें छः कोने A(0,0,0),B(L,0,0),C(L,L,0),DO,L,0),E(0,L,L) तथा F(0.0,L) पर हैं। इस क्षेत्र में एक चुम्बकीय क्षेत्र B=B0(ˆi+ˆk) टेस्ला विद्यमान है। लूप ABCDEFA से गुजरने वाला फ्लक्स है
View SolutionA loop, made of straight edges has six corners at A(0,0,0), B(L,0,0) ,C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field →B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edges has six corners at A(0,0,0), B(L, O,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionExplain giving reasons which of the following sets of quantum number are not possible
(a ) n=0, l =0 ml=0,ms=+12
( b) n=1 , l = 0 ml=0,ms=−12
( c) n=1,l=1,ml=0,ms=+12
(d ) n=2,l=1,ml=0,ms=12
( e) n=3, l = 3, ml=3,ms=+12
(f ) n=3, l = 1, ml=0,msl=+12
View Solution
