A loop, made of straight edges has six corners at A(0,0,0), B(L,0,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field →B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is:
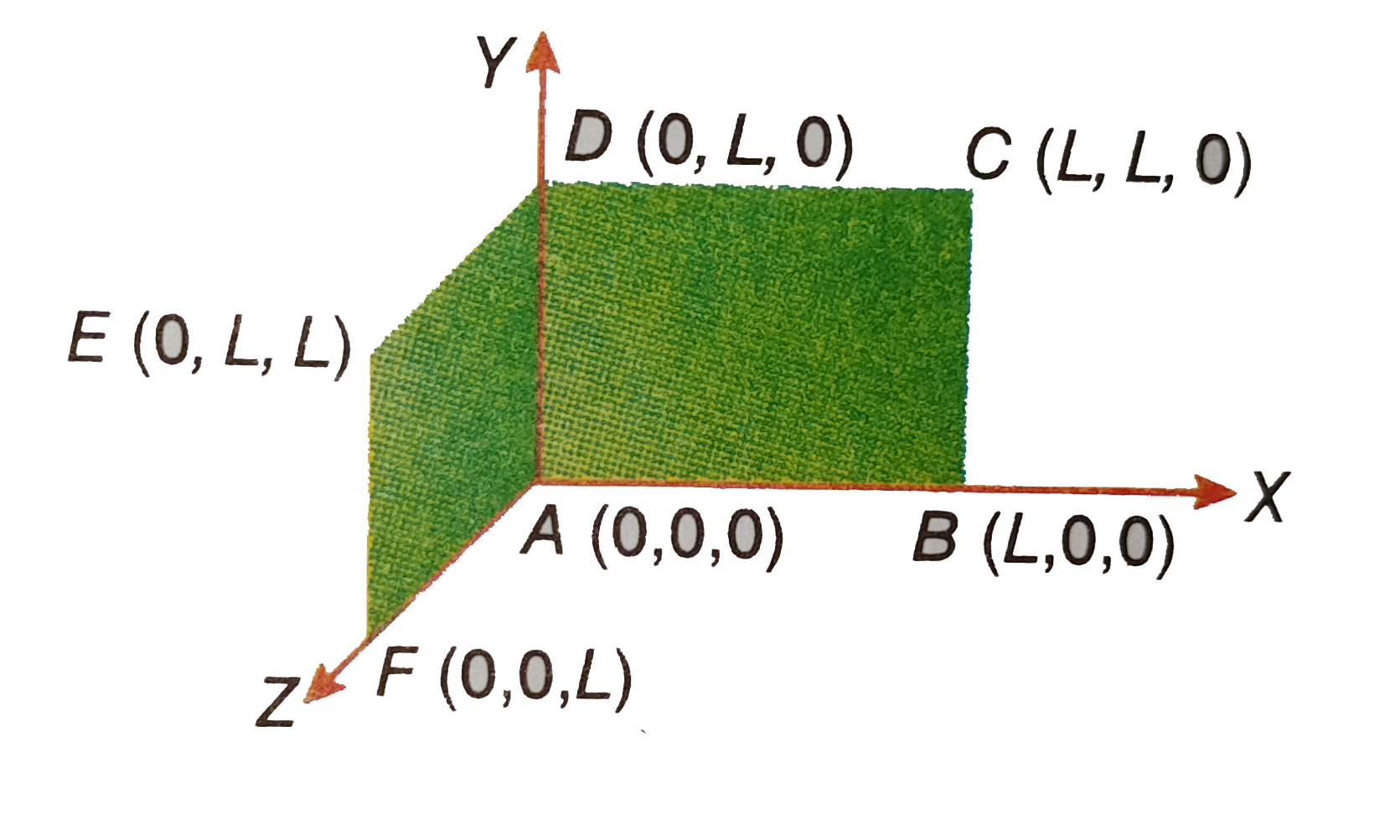 Solution in Bengali
Solution in Bengali
B0L2Wb
2B0L2Wb
√2B0L2Wb
4B0L2Wb
The correct Answer is:B
→A=L2ˆk+L2ˆi=L2(ˆi+ˆk)
∴ϕ=→B.→A=B0(ˆi+ˆk).L2(ˆi+ˆk)=2B0L2Wb
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT (MCQ-2)
4 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - EXERCISE
19 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - NCERTS TEXTBOOK QUESTIONS WITH ANSWER HINT
21 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
- ELECTROMAGNETIC WAVES BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER
17 Videos
Similar Questions
A metal plate is getting heated. It can be because
View SolutionIf the emf induced in an electrical circuit be e and the current induced be I then,
View SolutionUse Lenz's law to determine the direction of induced current in the situations described in the figure :

A wire of irregular shape turning into a circular shape.
View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.
View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
View SolutionA loop made of straight edegs has six corners at A(0,0,0), B(L, O,0) C(L,L,0), D(0,L,0) E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionConsider a loop ABCDEFA. With coordinates A (0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0) E(0, 5, 5) and F(0, 0, 5). Find magnetic flux through loop due to magnetic field vecB = 3 hati+4 hatk
View SolutionIf A=⎡⎢ ⎢ ⎢⎣k2000l2000m4⎤⎥ ⎥ ⎥⎦andA−1=⎡⎢ ⎢ ⎢⎣120001300014⎤⎥ ⎥ ⎥⎦ then k+l+m=
View SolutionA loop ABCA of straight edges has three corner points A (8, 0, 0), B (0, 8, 0 ) and C (0, 0, 8). The magnetic field in this region is →B=5(ˆi+ˆj+ˆk)T0 . The quantity of flux through the loop ABCA (in Wb) is _____.
View SolutionA loop made of straight edegs has six corners at A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L) and F(0,0,L). Where L is in meter. A magnetic field B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View Solutionसीधी कोरों से बने एक लूप में A(0, 0, 0), B(L, 0, 0), C(L, L, 0), D(0, L, 0), E(0, L, L), F(0, 0, L) पर छह कोने हैं। एक चुम्बकीय क्षेत्र →B=B0(ˆi+ˆk)T क्षेत्र में उपस्थित है। लूप ABCDEFA (उसी क्रम में) से गुजरने वाला फ्लक्स होगा-
View Solutionएक लूप सीधी भुजाओं से बना है, जिसमें छः कोने A(0,0,0),B(L,0,0),C(L,L,0),DO,L,0),E(0,L,L) तथा F(0.0,L) पर हैं। इस क्षेत्र में एक चुम्बकीय क्षेत्र B=B0(ˆi+ˆk) टेस्ला विद्यमान है। लूप ABCDEFA से गुजरने वाला फ्लक्स है
View SolutionA loop, made of straight edges has six corners at A(0,0,0), B(L,0,0) ,C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L). A magnetic field →B=B0(ˆi+ˆk)T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionA loop made of straight edges has six corners at A(0,0,0), B(L, O,0), C(L,L,0), D(0,L,0), E(0,L,L) and F(0,0,L) . Where L is in meter. A magnetic field B = B_(0)(hat(i) + hat(k))T is present in the region. The flux passing through the loop ABCDEFA (in that order) is
View SolutionConsider a loop ABCDEFA. With coordinates A (0, 0, 0), B(5, 0, 0), C(5, 5, 0), D(0, 5, 0) E(0, 5, 5) and F(0, 0, 5). Find magnetic flux through loop due to magnetic field →B=3ˆi+4ˆk
View Solution
