ABC ত্রিভুজে AB=9 সেমি., BC=6 সেমি CA=7.5সেমি । DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF, EF=8সেমি. এবং △DEF~ △ABC হলে △DEF-এর পরিসীমা
22.5 সেমি.
25 সেমি.
27 সেমি.
30 সেমি.
The correct Answer is:D
Step by step video & image solution for ABC ত্রিভুজে AB= 9 সেমি., BC= 6 সেমি CA=7.5সেমি । DEF ত্রিভুজে BC বাহুর অনুরূপ বাহু EF, EF=8সেমি. এবং /_\ DEF~ /_\ ABC হলে /_\ DEF-এর পরিসীমা by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
△ABC -এর BC -এর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে প্রমাণ করো যে,ABDB=ACEC
View Solutionআমি একটি মুখবন্ধ লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভুমির ব্যাসার্ধের দৈর্ঘ্য 15 সেমি এবং তির্যক উচ্চতা 24 সেমি| ওই শঙ্কুর পার্শ্ব তলের ক্ষেত্রফল ও সমগ্রতলের ক্ষেত্রফল হিসাব করে লেখো|
View SolutionIf Delta ABC-Delta DEF,BC=3cm,EF=4cm and area of Delta ABC=54sqcm then find the area of Delta DEF
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are similar triangles such that AB=3cm , BC=2cm CA=2.5cm and EF=4cm , write the perimeter of DEF .
View SolutionIn the figure, BA|| ED and BC|| EF. Show that ∠ABC = ∠DEF.
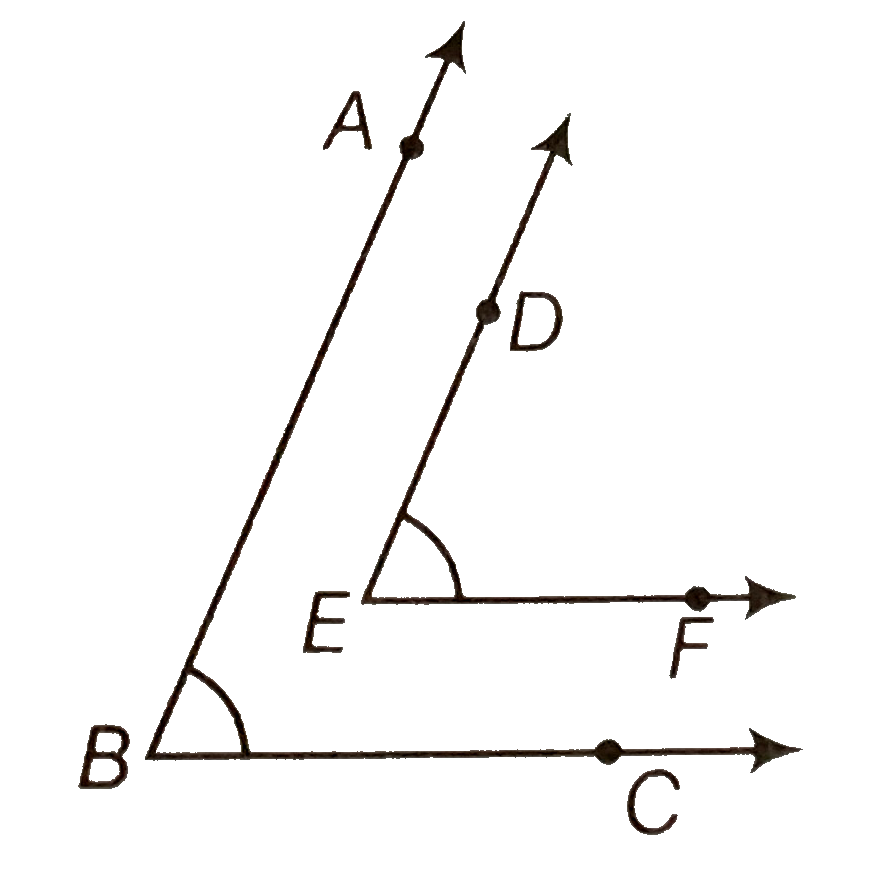
View SolutionIn ΔABC, it is given that AB=9cm,BC=6cm,andCA=7.5cm. AlsoΔDEF is givne such that EF=8cmandΔDEF~ΔABC. Then perimeter of ΔDEF is
View Solutionयदि ΔABC तथा ΔDEF दो समरूप त्रिभुज इस प्रकार है की ABDE=BCEF=CAFD=34 है| त्रिभुजों ABC तथा DEF का अनुपात ज्ञात करो|
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि ABDE=BCEF=CAFD=25 तो ar(ΔABC):ar(ΔDEF)=
View SolutionIn two triangle ABC and DEF, AB= DE ,BC=DF and AC =Ef then
View SolutionIn /_\ ABC and /_\ DEF , if AB=DE , BC=EF . Are they congruent?
View Solution△ABC ও △DEF-এর পরিসীমা যথাক্রমে 30 সেমি। এবং 18 সেমি। △ABC~ △DEF, BC ও EF অনুরূপ বাহু। যদি BC =9সেমি. হয়, তাহলে EF= ________ সেমি.।
View Solution△ABCও △DEF-এ ABDE=BCFD=ACEFহলে,
View SolutionIn the figure, BA|| ED and BC|| EF. Show that ∠ABC = ∠DEF.

View SolutionIn Δs ABC and DEF, DE and AB∣∣DE, BC=EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (see figure). Show that : △ABC ~= △DEF
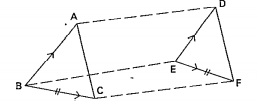
View Solution