নীচের বিবৃতিটি সত্য না মিথ্যা লেখ: -এর QR বাহুর উপর D এমন একটি বিন্দু যে , সুতরাং ~
Step by step video & image solution for নীচের বিবৃতিটি সত্য না মিথ্যা লেখ: /_\PQR-এর QR বাহুর উপর D এমন একটি বিন্দু যে PD bot QR, সুতরাং /_\PQD ~ /_\RPD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
△ABC -এর BC -এর সমান্তরাল সরলরেখা AB ও AC -কে যথাক্রমে D ও E বিন্দুতে ছেদ করলে প্রমাণ করো যে,ABDB=ACEC
View Solutionআমি একটি মুখবন্ধ লম্ব বৃত্তাকার শঙ্কু তৈরি করেছি যার ভুমির ব্যাসার্ধের দৈর্ঘ্য 15 সেমি এবং তির্যক উচ্চতা 24 সেমি| ওই শঙ্কুর পার্শ্ব তলের ক্ষেত্রফল ও সমগ্রতলের ক্ষেত্রফল হিসাব করে লেখো|
View SolutionD is a point on side QR of ΔPQR such that PD⊥QR. Will it be correct to say that ΔPQD~ΔRPD? Why?
View SolutionIi ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionIn ∠PQR,PQ=6cm,PR=9cm and M is a point on QR such that it divides QR in the ratio 1:2PM⊥QR. Find QR.
View Solution△PQR में, PD⊥QR इस प्रकार है कि D, QR पर स्थित है | यदि PQ = a, PR = b,QD = c तथा DR = d, तो सिद्ध कीजिए कि (a+b)(a−b)=(c+d)(c−d)
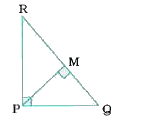
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR . Show that PM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR .
View SolutionIn ΔPQRsegPSis median ofΔPQR.AndPT⊥QR,
(i) PR2=PS2+QR×ST+(QR2)2
View SolutionIn ΔPQRsegPSis median ofΔPQR.AndPT⊥QR,
(ii)PQ2=PS2−QR×ST+(QR2)2
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionD is a point on side QR of ΔPQR such that PD⊥QR. Will it be correct to say that ΔPQD~ΔRPD? Why?
View SolutionIi ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionPQR is a Deltaright angled at P and M is a point on QR such that PM⊥QR. Show that PM2=QM⋅MR.
View Solution
