When a spring does work on an object, we cannot find the work by simple multiplying the spring force by the object's displacement. The reason is that there is no one value for the force-it changes. However, we can split the displacement up into an infinite number of tiny parts and then approximate the force in each as being constant. Integration sums the work done in all those parts. Here we use the generic result of the integration.
In Fig. 8-13, a cansiter of mass m = 0.40 kg slides across a horizontal frictionless counter with speed v = 0.50 m/s. It then runs into and compresses a spring of spring constant k = 750 N/m. When the canister is momentarily stopped by the spring, by what distance d is the spring compressed?
KEY IDEA
1. The work Ws done on the canister by the spring force is related to the requested distance d by
Eq. 8-26 (Ws=−1/2kx2) , with d replacing x.
2. The work Ws is also related to the Kinetic energy of the cansiter by Eq. 8-10 (Kf−Ki=W).
3. The cansiter.s Kinetic energy has an initial value of K=1/2mv2 and a value of zero when the canister is momentarily at rest.
Calculations: Putting the first two of these ideas together, we write the work-kinetic energy theorem for the canister as
Kf−Ki=−12kd2.
Substituting according to the third key idea gives us this expression:
0−12mv2=−12kd2.
Simplifying, solving for d, and substituting known data then give us
d=v√mk=(0.50m/s)√0.40kg750N/m
=1.2×10−2m=1.2cm.
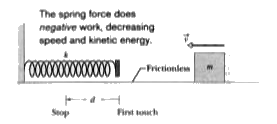
Figure 8-13 A canister moves toward a spring.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
Knowledge Check
Work done by a force on an object is zero, if
Athe force is always perpenicular to its accelerationBthe object is stationary but the point of application of the force moves on the objectCthe force is always perpendicular to its velocityDthe object moves in such a way that the point of application of the force remains fixedAssertion , No work is done if the displacement is zero
Reason: Work done by the force is defined to be the product of component of the force in the the direction of the displacement and the magnitude of displacement.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion and reason are false.
How is work done by a force measured when the force :
is in the direction of displacement.
View SolutionWork done by a force on an object is zero, if
View SolutionWhen the force on a object depends on the position of the object, we cannot find the work done by it on the object by simple multiplying the force by the displacement. The reason is that there is no one value for the force-it changes. So, we must find the work in tiny little displacements and then add up all the workk results. We effectively say, "Yes, the force varies over any given tiny little displacement. but the variation is so small we can approximate the force as being constant during the displacements infinitesimal, then our error becomes infinitesimal and the result becomes precise. But, to add an infinite number of work contributions by hand would take us forever, longer than a semester.So we add them up via an integration, which allows us to do all this in minutes (much less than a semester).
Force →F=(3x2N)ˆi+(4N)ˆj, with x in meters, acts on a particle, changing only the kinetic energy of th particle. How much work is done on the particle as it moves from coordinates (2 , 3 m) to 3 m, 0 m)? Does the speed of the particle increase, decrease, or remain the same?
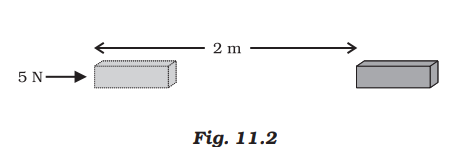
View SolutionA force of 5 N is acting on an object. The object is displaced through 2 m in the direction of the force (Fig. 11.2). If the force acts on the object all through the displacement, then work done is 5N×2m=10N m or 10J.
View SolutionHow is the work done by a force measured when (i) force is in the direction of displacement, (ii) force is at an angle to the direction of displacement ?
View SolutionWork done by a spring force is
View Solution
