Figure 8-32 shows a water-slide ride in which a glider is shot by a spring along a water-drenched (frictionless) track that takes the glider from a horizontal section down to ground level. As the glider then moves along the ground-level track, it is gradually brought to rest by friction. The total mass of the glider and its rider is m=200kg, the initial compression of the spring is d=5.00m, the spring constant is k=3.20×103 N/m, the initial height is h=35.0 m, and the coefficient of kinetic friction along the ground-level track is μs=0.800. Through what distance L does the glider slide along the ground-level track until it stops?
KEY IDEA
First of all we need to examine all the forces and then determine what our system should be. Only then can we decide what equation to wirte. Do we have an isolated system (our equation would be for the conservation of energy) or a system on which an external force does work (our equation would relate that work to the system.s change in energy ?
Forces : The normal force o the glider from the track does no work on the glider because the direction of this force is always perpendicular to the direction of the glider.s displacement. The gravitational force does work on the glider, and because the force is conervative we can associate a potential energy with it. As the spring pushes on the glider to get it moving, a spring force does work on it, transferring energy from the elastic potential energy of the compressed spring to kinetic energy of the glider. The spring force also pushes against a rigid wall. Because there is friction between the glider and the ground-level track, the sliding of the glider along that track section increases their thermal energies.
System : Let.s take the system to contain all the interacting bodies: glider, track, spring, Earth, and wall. Then, because all the force interactions are within the system, the system is isolated and thus its total energy cannot change. So, the equation we should use is not that of some external force doing work on the system. Rather, it is a conservation of energy. We write this in the form of
Emec,2=Emec,1−ΔEth.
This is like a money equation : The final money is equal to the initial money minus the amount stolen away by a thief. Here, the final mechanical energy is equal to the initial mechanical energy minus the amount stolen away by friction. None has magically appeared or disappeared.
Calculations : Now that we have an equation, let.s find distance L. Let subscript 1 correspond to the initial state of the glider (when it is still on the compressed spring) and subscript 2 correspond to the final state of the glider (when it has come to rest on the ground-level track).
For both states, the mechanical energy of the system is the sum of any potential energy and an kinetic energy.
We have two types of potential energy : the elastic potential energy (Ue=(1/2kx2) associated with the compressed spring and the gravitional potential energy (Ug=mgy) associated with the glider.s elevation. For the latter, let.s take ground level as the reference level. That means that the glider initially at height y = h and finally at height y = 0.
In the initial state, with the glider stationary and elevated and the spring compressed, the energy is
Emec,1=K1+Ue1+Ug1
=0+12kd2=mgh.
In the final state, with the spring now in its relaxed state and the glider again stationary but no longer elevated the final mechanical energy of the system is
Emec,2=K2+Ue2+Ug2
=0+0+0.
Let.s next go after the change ΔEth of the thermal energy of the glider and ground-level track. we can substitute for ΔEth with fkL (the product of the frictional force magnitude and the distance of rubbing). We know that fk=μkFN, where FN is the normal fore. Because the glider moves horizontally through the region with friction, the magnitude of FN is equal to mg (the upward force matches the downward force). So, the friction.s theft from the mechanical energy amounts to
ΔEth=μkmgL.
(By the way, without further experiments, we cannot say how much of this thermal energy ends up in the glider and how much in the track. We simply know the total amount.)
0=12kd2+mgh−μ2mgL.
and
L=kd22μkmg+hμk
=(3.20×103N/m)(5.00m)22(0.800)(200kg)(9.8m/s2)+35m0.800
=63.3m
Finally, note how algebraically simple our solution is. By carefully defining a system and realizing that we have an isolated system, we get to use the law of the conservation of energy. That means we can relate the initial and final states of the system with no consideration of the intermediate states. In particular. we did not need to consider the glider as it slides over the uneven track. If we had, instead, applied Newton.s second law to the motion, we should have had to know the details of the track and would have faced a far more difficult calculation.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View Solution
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View Solution
Knowledge Check

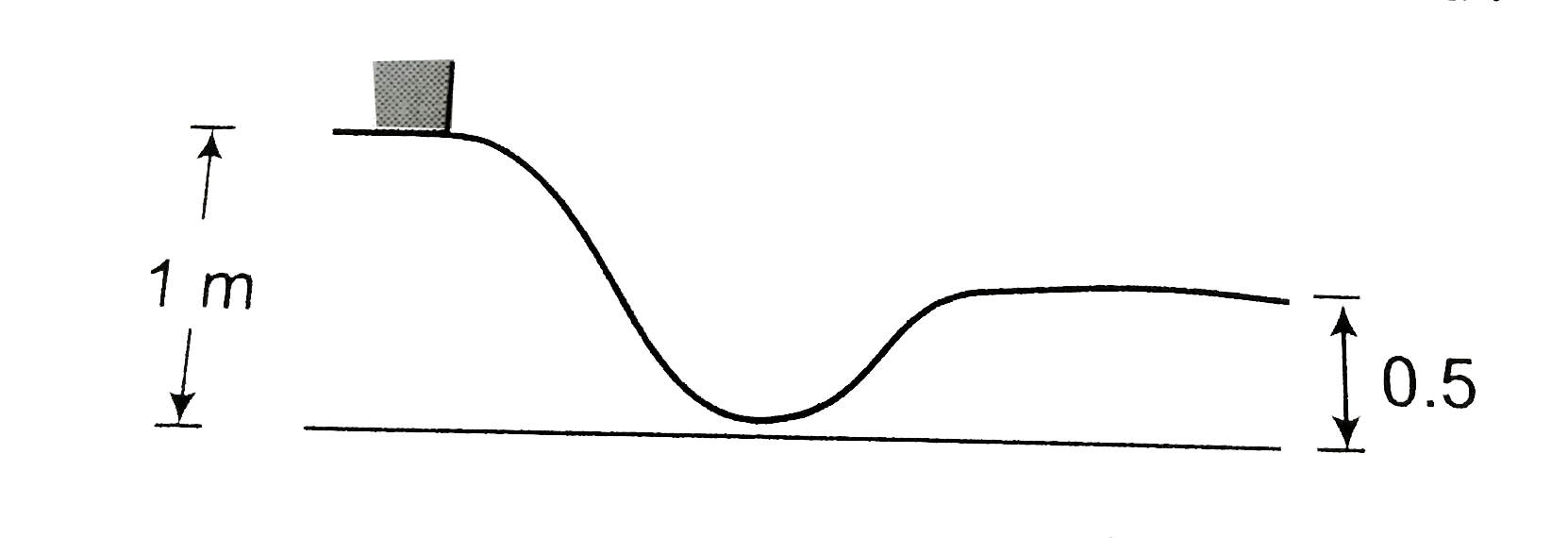
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?A1mB2mC3mD4mIn the figure, a block slides along a track from one level to a higher level, by inoving through an intermediate valley. The track is frictionless untill the block reaches the higher level. There a frictional force stops the block in a distance d. The block's initial speed v0 is 8 m/s, the height difference h is 2 m and the coefficient of kinetic friction μ is 0.3. The value of d is
 A4 mB3 mC5 mD8 m
A4 mB3 mC5 mD8 m
Figure shows a particle slideing on a frictionles track which terminates in straight horizontal section. If the particle starts slipping from the point. A, how far way from the track will the particle hit the ground ?
View SolutionFigure, a block slides along a track from one level to a higher level by moving through an intermediate valley. The track is friction less until the block reaches the higher
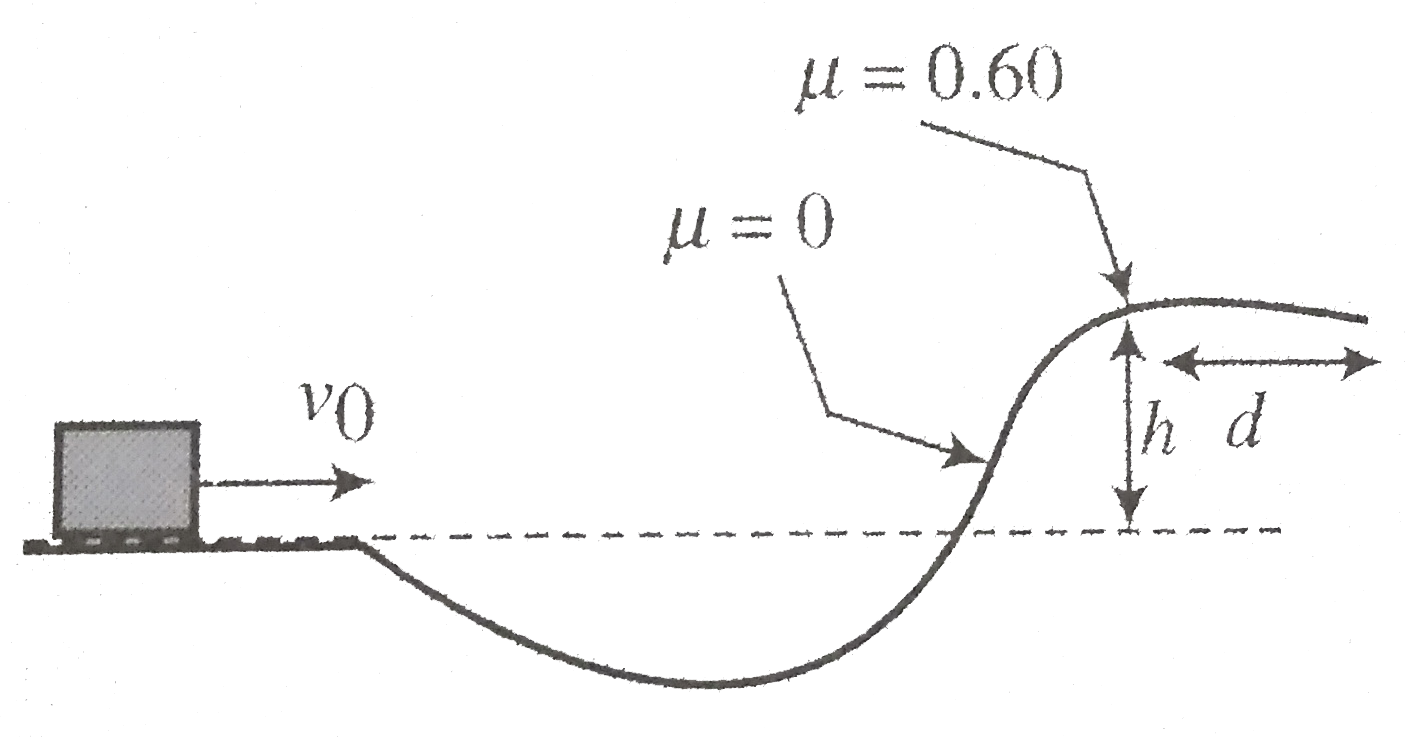 level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
View SolutionFigure, a block slides along a track from one level to a higher level by moving through an intermediate valley. The track is friction less until the block reaches the higher
 level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
level. Then there is friction force which stops the block at a distance d. The block's initial speed v0 is 6.0ms−1, the height difference h is 1.1m, and the coefficient of kinetic friction μ is 0.60. Find d.
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.
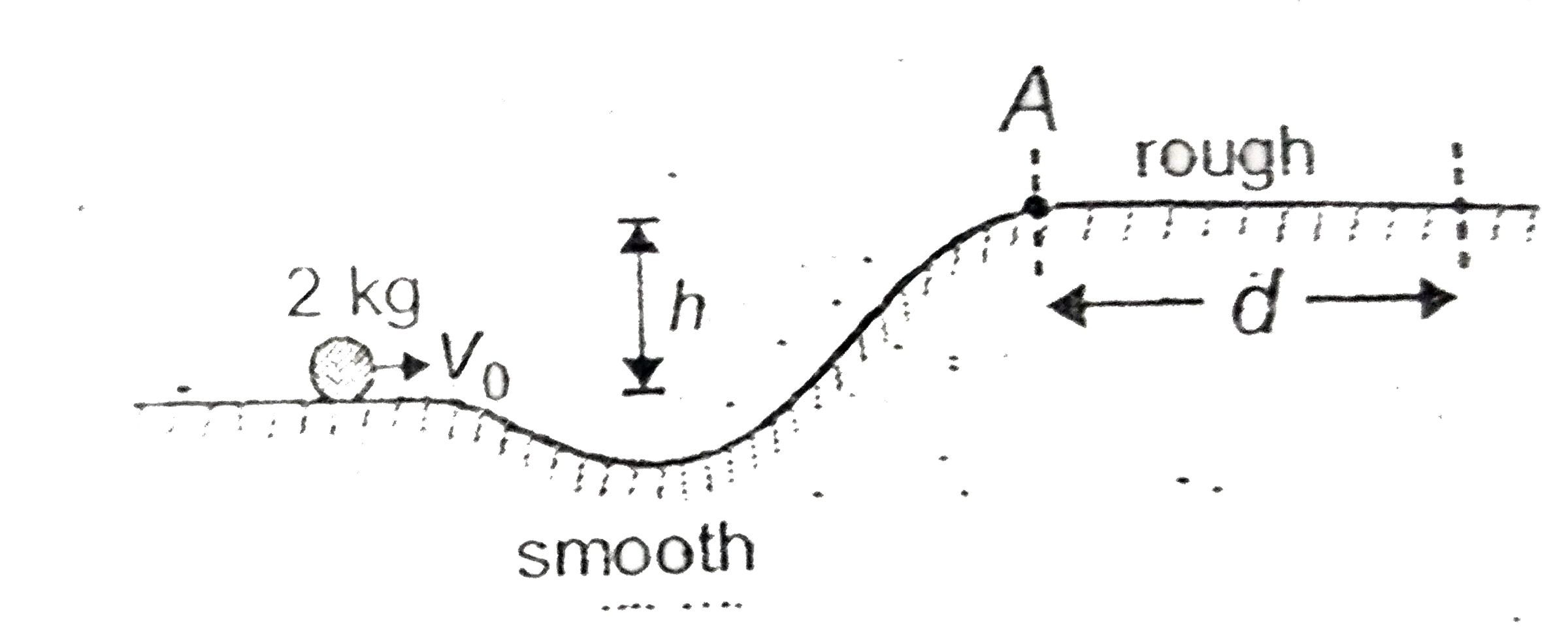
The speed of body at the higher level A is
View SolutionIn the arrangement show in figure, the track is frictionless until the body reaches the higher level. A frictional force stops the body in a distance d from A. The initial speed of the body v0 is 6 m/s the height h is 1 m and the coefficient of kinetic friction is 0.2.

The speed of body at the higher level A is
View SolutionIn figure-3.13, a block slides along a track from one level to a higher level, by moving through an intermediate valley. The track is frictionless until the block reaches the higher level. There a frictional force stops the block in a distance d. The block's initial speed v0 is 6m/s the height difference h is 1.1 m and the coefficient of kinetic friction μ is 0.6 find d. Take g=10m/s2

View Solution
