A fully loaded, slow-moving freight elevator has a cab with a total mass of 1200 kg, which is required to travel upward 54 m in 3.0 min, starting and ending at rest. The elevator's counterweight has a mass of only 950 kg, and so the elevator motor must help. What average power is required of the force the motor exerts on the cab via the cable ?
The correct Answer is:No work is required by the motor.
To solve the problem of determining the average power required by the elevator motor, we can follow these steps:
Step 1: Convert Time to Seconds
The time given for the elevator to travel upward is 3.0 minutes. We need to convert this time into seconds for our calculations.
Time in seconds=3.0min×60s/min=180s
Hint: Always convert time into seconds when working with power calculations in physics.
Step 2: Calculate the Weight of the Elevator and Counterweight
The weight of the elevator cab can be calculated using the formula:
Weight of the elevator(We)=me⋅g
where me=1200kg and g=9.81m/s2.
We=1200kg×9.81m/s2=11772N
The weight of the counterweight can be calculated similarly:
Weight of the counterweight(Wc)=mc⋅g
where mc=950kg.
Wc=950kg×9.81m/s2=9319.5N
Hint: Remember to use the acceleration due to gravity (approximately 9.81m/s2) when calculating weight.
Step 3: Determine the Net Force Acting on the Elevator
The net force that the motor must overcome is the difference between the weight of the elevator and the weight of the counterweight:
Fnet=We−Wc=11772N−9319.5N=2442.5N
Hint: The motor needs to exert enough force to not only lift the elevator but also to counteract the weight of the counterweight.
Step 4: Calculate the Work Done by the Motor
The work done by the motor can be calculated using the formula:
Work(W)=Fnet⋅d
where d=54m.
W=2442.5N×54m=132,045J
Hint: Work is the product of force and displacement in the direction of the force.
Step 5: Calculate the Average Power Required
Power is defined as the work done per unit time:
Power(P)=Wt
Substituting the values we have:
P=132,045J180s≈733.5W
Hint: Power is a measure of how quickly work is done, so always divide the total work by the time taken.
Final Answer
The average power required of the force the motor exerts on the cab via the cable is approximately 733.5 W.
The time given for the elevator to travel upward is 3.0 minutes. We need to convert this time into seconds for our calculations.
The weight of the elevator cab can be calculated using the formula:
where me=1200kg and g=9.81m/s2.
where mc=950kg.
The net force that the motor must overcome is the difference between the weight of the elevator and the weight of the counterweight:
The work done by the motor can be calculated using the formula:
where d=54m.
Power is defined as the work done per unit time:
The average power required of the force the motor exerts on the cab via the cable is approximately 733.5 W.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)59videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)10videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT6videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)4videos
WAVES-I
Similar Questions
Which one of the following statements about kinetic energy is true ?
03:51View SolutionA boy pulls 5 kg block by 20 m along a horizontal surface at constant speed with a force directed 45∘ above the horizontal. If the coefficient of friction is 0.2, then
01:33View SolutionA lift is going up with constant velocity v0. Calculate the work done by normal force Fg from the reference frame of ground and lift in time t.
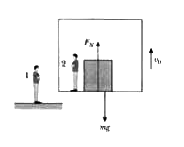 02:26View Solution
02:26View SolutionA progressive and a stationary simple harmonic wave each has the same frequency 250Hz and the same velocity of 30m/s. Calculate the distance between consecutive nodes (in cm) in the stationary wave.
03:16View SolutionThe total mass of an elevator with a 80 kg man in it is 1000 kg. This elevator moving upward with a speed of 8 m//sec, is brought to rest over a distance of 16m. The tension T in the cables supporting the elevator and the force exerted on the man by the elevator floor will respectively be-
02:40View SolutionAn elevator with passengers has a total mass of 800 kg and moves slowly a vertical distance of 20.0 m in 10.0s . What is the average power expended in lifting this mass ?
02:57View SolutionAn elevator has mass of 600 kg, not including passengers The elevator is designed to ascend at constant speed a vertical distance of 20 m in 15 sec. It is driven by a motor that can provide up to 30 hp to the elevator, what is the maximum number of passengers that can ride in the elevator ? Assume that an average passenger has a mass of 65 kg
03:06View SolutionA lift of mass 920 kg has a capacity of 10 persons. If average mass of person is 68 kg. Friction force between lift and lift shaft is 6000 N. The minimum power of motor required to move the lift upward with constant velocity 3 m/s is [g=10ms2 ]
03:01View Solutionएक मोटरगाड़ी का द्रव्यमान 1200 kg है। यदि मोटर गाड़ी को 1.5m/s2 के ऋणात्मक त्वरण (negative acceleration), अर्थात के साथ विरामावस्था में लाना हो, तो मोटर गाड़ी और सड़क के बीच लगनेवाला घर्षण बल होगा
04:22View SolutionAn elevator cab is pulled upward by a cable. The cab and its single occupant have a combined mass of 2000 kg. When that occupant drops a coin, its acceleration relative to the cab is 8.30 m/s2 downward. What is the tension in the cable?
02:49View SolutionA woman stands on a scale in a moving elevator. Her mass is 60.0 kg, and the combined mass of the elevator and scale is an additional 815 kg. Starting from rest, the elevator accelerates upward. During the acceleration, the hoisting cable applies a force of 9410 N. What does the scale read during the acceleration ?
03:12View SolutionAn elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2 ms^(-1) . The friction force opposite the motion is 4000 N .What is minimum power delivered by the motor to the elevator?
02:40View SolutionThe loaded cab of an elevator has a mass of 5.0×103 kg and moves 210 m up the shaft in 23 s at constant speed. At what average rate does the force from the cable do work on the cab ?
View SolutionA lift of mass 920 kg has a capacity of 10 persons. If average mass of person is 68 kg. Friction force between lift and lift shaft is 6000 N. The minimum power of motor required to move the lift upward with constant velocity 3 m/s is [g=10ms2 ]
07:14View SolutionA lift of mass 920 kg has a capacity of 10 persons. If average mass of person is 68 kg. Friction force between lift and lift shaft is 6000 N. The minimum power of motor required to move the lift upward with constant velocity 3 m/s is [g=10ms2 ]
02:33View Solution

