A 55-kg box is being pushed a distance of 7.0 m across the floor by a force →p whose magnitude is 150 N. The force →P is parallel to the displacement of the box. The coefficient of kinetic friction is 0.25. Determine the work done on the box by each of the four forces that act on the box. Be sure to include the proper plus or minus sign for the work done by each force. ( The four forces and the force P, the frictional force f, the normal force N, and the force due to gravity mg. )
WpWfWNWmg1.0×103J−940J−3.8×103J3.8×103J
WpWfWNWmg1.0×103−940JzeroJzeroJ
WpWfWNWmgzeroJ940J−3.8×103J3.8×103J
WpWfWNWmg−1.0×103JzeroJzeroJ−3.8×103J
The correct Answer is:B
To solve the problem, we need to calculate the work done by each of the four forces acting on the box: the applied force →P, the frictional force →F, the normal force →N, and the gravitational force →W.
Step 1: Calculate the work done by the applied force →P
The work done by a force is given by the formula:
W=F⋅d⋅cos(θ)
where:
- F is the magnitude of the force,
- d is the displacement,
- θ is the angle between the force and the direction of displacement.
In this case, the applied force →P has a magnitude of 150 N and is parallel to the displacement (7.0 m), so θ=0∘.
WP=150N⋅7.0m⋅cos(0∘)=150⋅7⋅1=1050J
Step 2: Calculate the frictional force →F
The frictional force can be calculated using the formula:
F=μ⋅N
where μ is the coefficient of kinetic friction and N is the normal force. The normal force N is equal to the weight of the box, which is given by:
N=mg
where m=55kg and g=9.8m/s2.
Calculating N:
N=55kg⋅9.8m/s2=539N
Now, calculating the frictional force:
F=0.25⋅539N=134.75N
Step 3: Calculate the work done by the frictional force →F
The frictional force acts opposite to the direction of displacement, so θ=180∘.
WF=F⋅d⋅cos(180∘)=134.75N⋅7.0m⋅(−1)=−943.25J
Step 4: Calculate the work done by the normal force →N
The normal force acts perpendicular to the displacement, so θ=90∘.
WN=N⋅d⋅cos(90∘)=539N⋅7.0m⋅0=0J
Step 5: Calculate the work done by the gravitational force →W
The gravitational force also acts perpendicular to the displacement, so θ=90∘.
WW=W⋅d⋅cos(90∘)=mg⋅d⋅0=0J
Final Results:
- Work done by the applied force WP=1050J
- Work done by the frictional force WF=−943.25J
- Work done by the normal force WN=0J
- Work done by the gravitational force WW=0J
Summary of Work Done by Each Force:
- WP=+1050J
- WF=−943.25J
- WN=0J
- WW=0J
W=F⋅d⋅cos(θ)
where:
- F is the magnitude of the force,
- d is the displacement,
- θ is the angle between the force and the direction of displacement.
F=μ⋅N
where μ is the coefficient of kinetic friction and N is the normal force. The normal force N is equal to the weight of the box, which is given by:
N=mg
where m=55kg and g=9.8m/s2.
N=55kg⋅9.8m/s2=539N
F=0.25⋅539N=134.75N
- Work done by the frictional force WF=−943.25J
- Work done by the normal force WN=0J
- Work done by the gravitational force WW=0J
- WP=+1050J
- WF=−943.25J
- WN=0J
- WW=0J
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)10videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)9videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS58videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)4videos
WAVES-I
Similar Questions
A 3.5 kg block is pushed along a horizontal floor by a force →F of magnitude 15 N at an angle θ=40∘ with the horizontal (Fig. 6-33). The coefficient of kinetic friction between the block and the floor is 0.25. Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block's acceleration.
 View Solution
View SolutionA heavy box of mass 20 kg is pulled on a horizontal force.If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted by horizontal surface on the box.
View Solution
Knowledge Check
- Question 1 - Select One
A person is not able to push a box lying on the ground by applying a force. The force applied by the person is_____ static friction force.
Aless thanBgreater thanCequal toDnone of these - Question 2 - Select One
A 6.00 kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0.360. Determine the kinetic frictional force that acts on the box when the elevator is stationary.
A18.6NB22.4BC21.2ND23.8N - Question 3 - Select One
A 1.00×102 kg crate is being pushed across a horizontal floor by a force →P that makes an angle of 30.0∘ below the horizontal. The coefficient of kinetic friction is 0.200. What should be the magnitude of →P, so that the net work done by it and the kinetic frictional force is zero ?
A256NB354NC203ND287N
A box, heavier than you is placed on a rough floor. The coefficient of static friction between the box and the floor is the same as that between your shoes and the floor. Can you displace the box across.the floor.
View SolutionA person pushes horizontally with a force of 220 N on a 55 kg crate to move it across a level floor. The coefficient of kinetic friction between the crate and the floor is 0.35. What is the magnitude of (a) the frictional force?
View SolutionThe coefficient of kinetic friction between a 20 kg box and the floor is 0.40. How much work does a pulling force do on the box in pulling it 8.0 m across the floor at constant speed? The pulling force is directed 37∘ above the horizontal.
View SolutionFigure shows the top view of two horizontal forces pulling a box along the floor. The work done by each force to displace the box 70 cm along the broken line is :
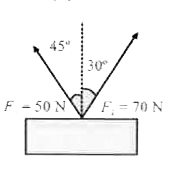 View Solution
View SolutionYou want to apply a force on a box so that it moves with constant speed across a horizontal floor. The coefficient if kinetic friction between the box and the floor is μk. Of the flur following cases, the force you apply on the box will be smallest when you
View Solution

