A skier slides horizontally along the snow for a distance of 21 m before coming to rest. The coefficient of kinetic friction between the stier and the snow is μk=0.050. Initially, how fast was the skier going ?
6.4m/s
4.5m/s
2.7m/s
5.4m/s
The correct Answer is:B
To solve the problem, we will use the concepts of work, energy, and friction. Here’s a step-by-step solution:
Step 1: Understand the forces acting on the skier
The skier is sliding on snow, and the only horizontal force acting on the skier is the frictional force, which opposes the motion. The coefficient of kinetic friction (μk) is given as 0.050.
Step 2: Write down the expression for the frictional force
The frictional force (Ff) can be calculated using the formula:
Ff=μk⋅m⋅g
where:
- μk=0.050 (coefficient of kinetic friction)
- m is the mass of the skier (which will cancel out later)
- g=10m/s2 (acceleration due to gravity)
Step 3: Calculate the work done by friction
The work done by friction (Wf) as the skier slides a distance s is given by:
Wf=−Ff⋅s
Substituting the expression for frictional force:
Wf=−(μk⋅m⋅g)⋅s
Step 4: Relate work done to change in kinetic energy
According to the work-energy principle:
Wf=ΔKE=KEf−KEi
Since the skier comes to rest, the final kinetic energy (KEf) is 0. The initial kinetic energy (KEi) is given by:
KEi=12mu2
Thus, we have:
−μk⋅m⋅g⋅s=0−12mu2
Step 5: Simplify the equation
Cancelling m from both sides (since m is not zero):
−μk⋅g⋅s=−12u2
Rearranging gives:
12u2=μk⋅g⋅s
Step 6: Solve for initial velocity u
Multiplying both sides by 2:
u2=2⋅μk⋅g⋅s
Substituting the known values:
- μk=0.050
- g=10m/s2
- s=21m
Calculating:
u2=2⋅0.050⋅10⋅21
u2=2⋅0.050⋅210
u2=21
Taking the square root:
u=√21≈4.58m/s
Final Answer
The initial speed of the skier was approximately 4.58m/s.
---
The skier is sliding on snow, and the only horizontal force acting on the skier is the frictional force, which opposes the motion. The coefficient of kinetic friction (μk) is given as 0.050.
The frictional force (Ff) can be calculated using the formula:
Ff=μk⋅m⋅g
where:
- μk=0.050 (coefficient of kinetic friction)
- m is the mass of the skier (which will cancel out later)
- g=10m/s2 (acceleration due to gravity)
The work done by friction (Wf) as the skier slides a distance s is given by:
Wf=−Ff⋅s
Substituting the expression for frictional force:
Wf=−(μk⋅m⋅g)⋅s
According to the work-energy principle:
Wf=ΔKE=KEf−KEi
Since the skier comes to rest, the final kinetic energy (KEf) is 0. The initial kinetic energy (KEi) is given by:
KEi=12mu2
Thus, we have:
−μk⋅m⋅g⋅s=0−12mu2
Cancelling m from both sides (since m is not zero):
−μk⋅g⋅s=−12u2
Rearranging gives:
12u2=μk⋅g⋅s
Multiplying both sides by 2:
u2=2⋅μk⋅g⋅s
Substituting the known values:
- μk=0.050
- g=10m/s2
- s=21m
u2=2⋅0.050⋅10⋅21
u2=2⋅0.050⋅210
u2=21
u=√21≈4.58m/s
The initial speed of the skier was approximately 4.58m/s.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A bullet of mass 10 gram is fired horizontally into a 5 kg wooden block at rest on a horizontal surface The coefficient of kinetic friction between the block and the surface is 0.1 Calculate the speed of the bullet striking the block if the combination moves 20 m before coming rest .
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
View Solution
Knowledge Check
A 6.00 kg box is sliding across the horizontal floor of an elevator. The coefficient of kinetic friction between the box and the floor is 0.360. Determine the kinetic frictional force that acts on the box when the elevator is stationary.
A18.6NB22.4BC21.2ND23.8NA block of mass m sliding down an inclined at constant speed is initial at a height h shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is μ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?
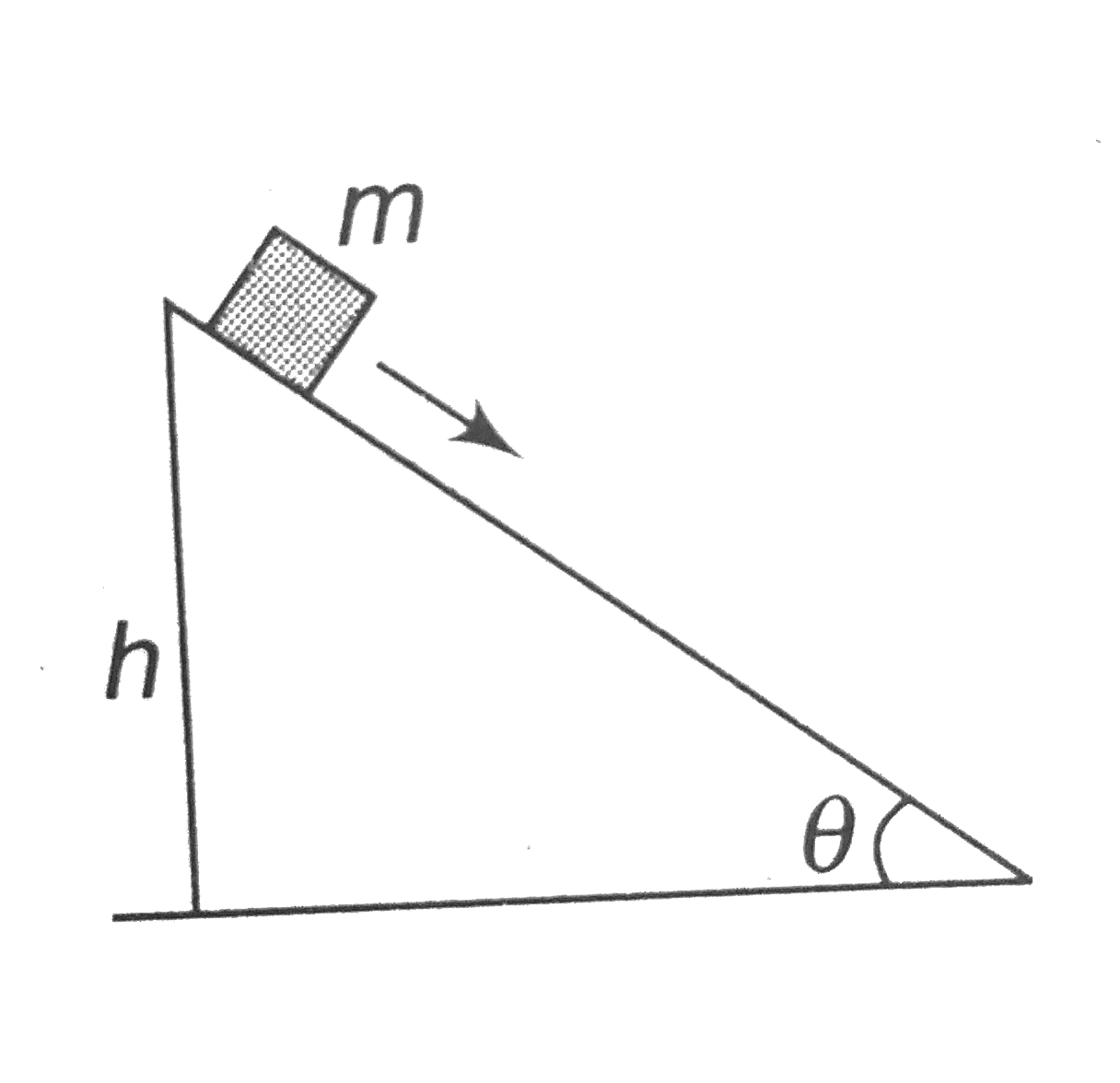 Amgh/θBmghCμmgh/sinθDmghsinθ
Amgh/θBmghCμmgh/sinθDmghsinθA block placed on a rough harizontal surface is imparted a velocity of 10 m/s. the coefficient of kinetic friction between the block and the surface is 0.5 and g=10m/s2. How much distance the block will cover, before coming to rest?
A5 mB7.5 mC12 mD10 m
A bullet of mass 0.01 kg is fired horizontal into a 4 kg wooden block block at rest , on a horizontal surface. The coefficient of kinetic friction between the block and surface is 0.25 the combination moves 20 m before coming to rest . With what speed did the bullet strike the block ?
View SolutionA block slides down an incline of 30∘ with the horizontal starting from rest it covers 8m in the first two seconds Find the coefficient of kinetic friction between the two .
View SolutionA bullet fired horizontally with a speed of 400m/sec. It strikes a wooden block of mass 5kg initially at rest placed on a horizontal floor as shown in the figure.It emerges with a speed of 200m/sec and the block slides a distance 20cm before coming to rest.Find the coefficient of friction between block and the surface.Mass of bullet is 20g . (take g=10ms2)
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionThe brakes of a car moving at 20 m/s along a horizontal road are suddenly applied and it comes to rest after travelling some distance if the coefficient of friction between the tyres and the road is 0.90 and it is assumed that all four tyres behave identically, the shortest distance the car would travel before coming to a stop is
View Solution
