दो पदार्थों जिनके ऊष्मा चालकता गुणांक K तथा 2K तथा मोटाई क्रमशः x तथा 4x है, को जोड़कर एक संयुक्त पटिका बनायी गयी है, जिसके दो बाहा पृष्ठों के ताप, क्रमश: T1 तथा T2(T2>T1) है। स्थायी अवस्था में इस पदिटका से प्रवाहित ऊष्मा की दर (A(T2−T1)Kx)f है.
जिसमे f का मान है

1
12
23
13
The correct Answer is:D
माना उभयनिष्ठ सतह का ताप T∘C है।
ऊष्मा प्रवाह की दर
H=Qt=KAΔTl
∴H1=(Qt)t=2KA(T−T1)4x
H2=(Qt)t=KA(T2−T)x
स्थायी अवस्था में पूरे निकाय में ऊष्मा प्रवाह की दर समान होगी।
H1=H2
⇒2KA(T−T1)4x=KA(T2−T)x
⇒T−T12=T2−T
⇒T−T1=2T2−2T
⇒T=2T2+T13 .....(i)
अतः स्लैब के लिए ऊष्मा प्रवाह की दर
H=[KA(T2−T)x]=KAx(T2−2T2+T13)=KA3x(T2−T1) ....(ii)
H=[A(T2−T1)Kx]f
समी (ii) व (iii) की तुलना करने पर
f=13
Topper's Solved these Questions
- गैसों का अणुगति सिद्धान्तBOOK - ARIHANT HINDICHAPTER - गैसों का अणुगति सिद्धान्तEXERCISE - प्रश्नावली (स्तर 2 (दृढ़कथन-कारण प्रकार))
11 Videos
- गुरुत्वाकर्षण BOOK - ARIHANT HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - प्रश्नावली (विगत वर्षों के प्रश्न)
11 Videos
- घूर्णन BOOK - ARIHANT HINDICHAPTER - घूर्णन EXERCISE - प्रश्नावली (विगत वर्षो के प्रश्न)
22 Videos
Similar Questions
वक्तव्य I स्टीफन नियतांक का SI मात्रक Wm−2K−4 है।
वक्तव्य II स्टीफन का नियम E=αT4
View Solutionएक अन्तरिक्षयान का द्रव्यमान 1000 किग्रा है | इसका पृथ्वी के पृष्ठ से स्वतंत्र अन्तरिक्ष में प्रमोचन किया जाना है | g एवं R (पृथ्वी की त्रिज्या ) के मान क्रमशः 10 10मी / से2 और 6400 किमी हैं | इस कार्य के लिये आवश्यक ऊर्जा होगी
View Solutionएक द्विपरमाणुक अणु m1 तथा m2 के दो द्रव्यमानो से बना है जोको दूरी r पर है यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकार हम इसकी घूर्णन ऊर्जा की गणना करें तब इसकी ऊर्जा दी जाएगी (n एक पूर्णांक है)
View Solutionउस अनुक्रम का प्रथम पाँच पद निकालिए जिसके लिए
t1=1,t2=2 तथा tn+2=tn+tn+1.
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक पुस्तकालय को एक शेल्फ में दो भिन्न प्रकार की पुस्तकें रखनी है| पुस्तकें क्रमशः 6 सेमि और 4 सेमि मोती है| तथा उसका भार क्रमशः 1 किग्रा और 112 किग्रा है| शेल्फ 96 सेमि लम्बी है तथा अधिकतम 21 किग्रा भार सेह सकती है|शेल्फ दो प्रकार की पुस्तकों से किस प्रकार भरा जाएँ ताकि उसमें अधिकतम पुस्तकें रखी जा सकें?
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionयदि α=(λ−2)a+b तथा β=(4λ−2)a+3b दो दिए गए सदिश है, जहाँ सदिश a तथा b सरीख नहीं है । λ का वह मान जिसके लिए α तथा β सरीख है, है
View SolutionCO2 गैस का T1K पर औसत वेग (average velocity) तथा T2K पर अधितकम प्रायिकता वेग (most probable velocity ) 9.0×104 सेमी से−1 है।
T1 तथा T2 के मानों की गणना कीजिए।
View SolutionLet Tk=3(k+2)(k+3). Then (T1+T2+T3+......infinite terms) = ?
View SolutionLet Tk=sinkx+coskxFor all x if T1T5+T3T5=T1T7+T3Tnthen n=
View Solutionदो पदार्थों जिनके ऊष्मा चालकता गुणांक K तथा 2K तथा मोटाई क्रमशः x तथा 4x है, को जोड़कर एक संयुक्त पटिका बनायी गयी है, जिसके दो बाहा पृष्ठों के ताप, क्रमश: T1 तथा T2(T2>T1) है। स्थायी अवस्था में इस पदिटका से प्रवाहित ऊष्मा की दर (A(T2−T1)Kx)f है.
जिसमे f का मान है

View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
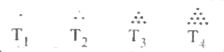
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionLet t1=(sin−1x)sin−1x,t2=(sin−1x)cos−1x,t3=(cos−1x)sin−1x,t4=(cos−1x)cos−1x
Match the items of Column I with the items Column II
Column-IColumn-IIA) x∈(0,cos1)p) t1>t2>t4>t3B) x∈(cos1,1√2)q) t4>t3>t1>t2C) x∈(1√2,sin1)r) t1>t2>t4>t3D) x∈(sin1,1)s) t3>t4>t1>t2
View Solution
