The profit fucntion in rupees of a firm selling x items (x≥0) per week is given by P(x)=−3500+(400−x)x How many items should the firm sell so that the firm has maximum profit ?
400
300
200
100
The correct Answer is:C
p(x)=−3500+(400−x)x=−3500+400x−x2
pone differentiationg w.r.t x we get
p(x) =400 -2x
Put p'(x) =0 for maxima or minima
→400−2x=0
→x=200
Now p''(x)=−2x
→P''(200)=−400<0
∴ p(x) is maximum at x=200
Hence 200 items should the firm sell so that the firm has maximum profit
Topper's Solved these Questions
Similar Questions
The profit function P(x) of a firm, selling x items per day is given by P(x)= (150−x)x−1625. Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit
View SolutionA manufacturer can sell x items at the price of Rs. (330−x) each. The cost of producing xitems is Rs. x2+10x−12. How many items must be sold so that his profit is maximum?
View Solution
Knowledge Check
The profit function, in rupees, of a firm selling t items (x≥0) per week is given by P(x)=−3500+(400−x)x. How many items should the firm sell so that the firm has maximum profit
A400B30C200D200A person sold 25 articles for Rs.2500 and incurred a loss of 10%. How many articles should he sell for Rs2400 to make a profit of 20%?
एक व्यक्ति ने 2500 रुपये में 25 वस्तुएँ बेची और उसे 10% की हानि हुई | उसे 2400 रुपये में कितनी वस्तुएँ बेचनी चाहिए ताकि 20% का लाभ हो ?Ars 500Brs 640Crs 540Drs 600Manufacturer can sell x items at a price of rupees (5−x100)each. The cost price of x items is Rs (x5+500). Find the number of items he should sell to earn maximum profit
Ax=140Bx=240Cx=340Dx=440
A producer can sell any quantity of a commodity at a given price of Rs. 10 per unit. His cost schedule is given below:
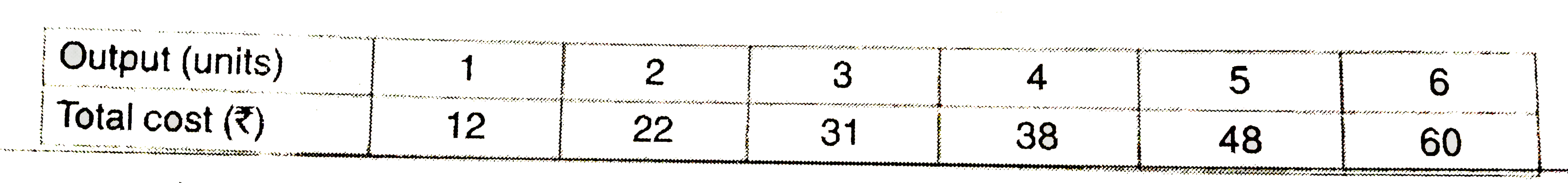
How many units should he produce to get maximum profit ? Explain.
View SolutionA manufacturer can sell 'x' items at a price of Rs (250−x) each. The cost of producing 'x' items is Rs (x2−50x+12). Determine the number of items to be sold so that he can make maximum profit.
View SolutionA manufacturer can sell x items at a price of Rs. (5−x100) each. The cost price of x items is Rs. (x5+ 500). Find the number of items he should sell to earn maximum profit.
View SolutionThe total cost C(x) of producing x items in a firm is given by C(x)=0.0005x3−0.002x2+30x+6000 Find the marginal cost when 4 units are produced
View SolutionA manufacturer can sell x items per month at a price p= Rs.(300-2x) Manufacturer's cost of production, Rs.y, of x items is given by y=2x+1000 . Find the number of items to be produced per month to yield the maximum profit.
View Solution
