The instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
3α+7β
32α+73β
α2+β3
32α+72β
To find the distance traveled by the particle between 1 second and 2 seconds, we start with the given instantaneous velocity function:
v(t)=αt+βt2
Step 1: Relate velocity to distance
We know that velocity is the derivative of distance with respect to time:
v=dsdt
Thus, we can express the differential distance ds as:
ds=vdt=(αt+βt2)dt
Step 2: Integrate to find distance
To find the total distance traveled between 1 second and 2 seconds, we need to integrate ds from t=1 to t=2:
s=∫21(αt+βt2)dt
Step 3: Perform the integration
Now we can integrate the function:
s=∫21(αt+βt2)dt=∫21αtdt+∫21βt2dt
Calculating each integral separately:
1. For the first integral:
∫αtdt=αt22
Evaluating from 1 to 2:
(α(2)22)−(α(1)22)=α(4)2−α(1)2=2α−α2=4α−α2=3α2
2. For the second integral:
∫βt2dt=βt33
Evaluating from 1 to 2:
(β(2)33)−(β(1)33)=β(8)3−β(1)3=8β−β3=7β3
Step 4: Combine the results
Now, we combine the results from both integrals to find the total distance s:
s=3α2+7β3
Final Result
Thus, the distance traveled by the particle between 1 second and 2 seconds is:
s=3α2+7β3
We know that velocity is the derivative of distance with respect to time:
To find the total distance traveled between 1 second and 2 seconds, we need to integrate ds from t=1 to t=2:
Now we can integrate the function:
Now, we combine the results from both integrals to find the total distance s:
Thus, the distance traveled by the particle between 1 second and 2 seconds is:
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION-B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
The position (in meters) of a particle moving on the x-axis is given by: x=2+9t+3t2−t3, where t is time in seconds . The distance travelled by the particle between t= 1s and t= 4s is m.
View SolutionA partical moves in a straight line as s=α(t−2)3+β(2t−3)4, where α and β are constants. Find velocity and acceleration as a function of time.
View Solution
Knowledge Check
If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
A32A+4BB3A+7BC32A+73BDA2+B3If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
A32A+4BB3A+7BC32A+73BDA2+B3The velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :A2mB3mC4mD6m
A particle starts from rest with acceleration a=αt+βt2 where α and β are constants. Find its displacement between t = 1 and t= 2 second.
View SolutionVelocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
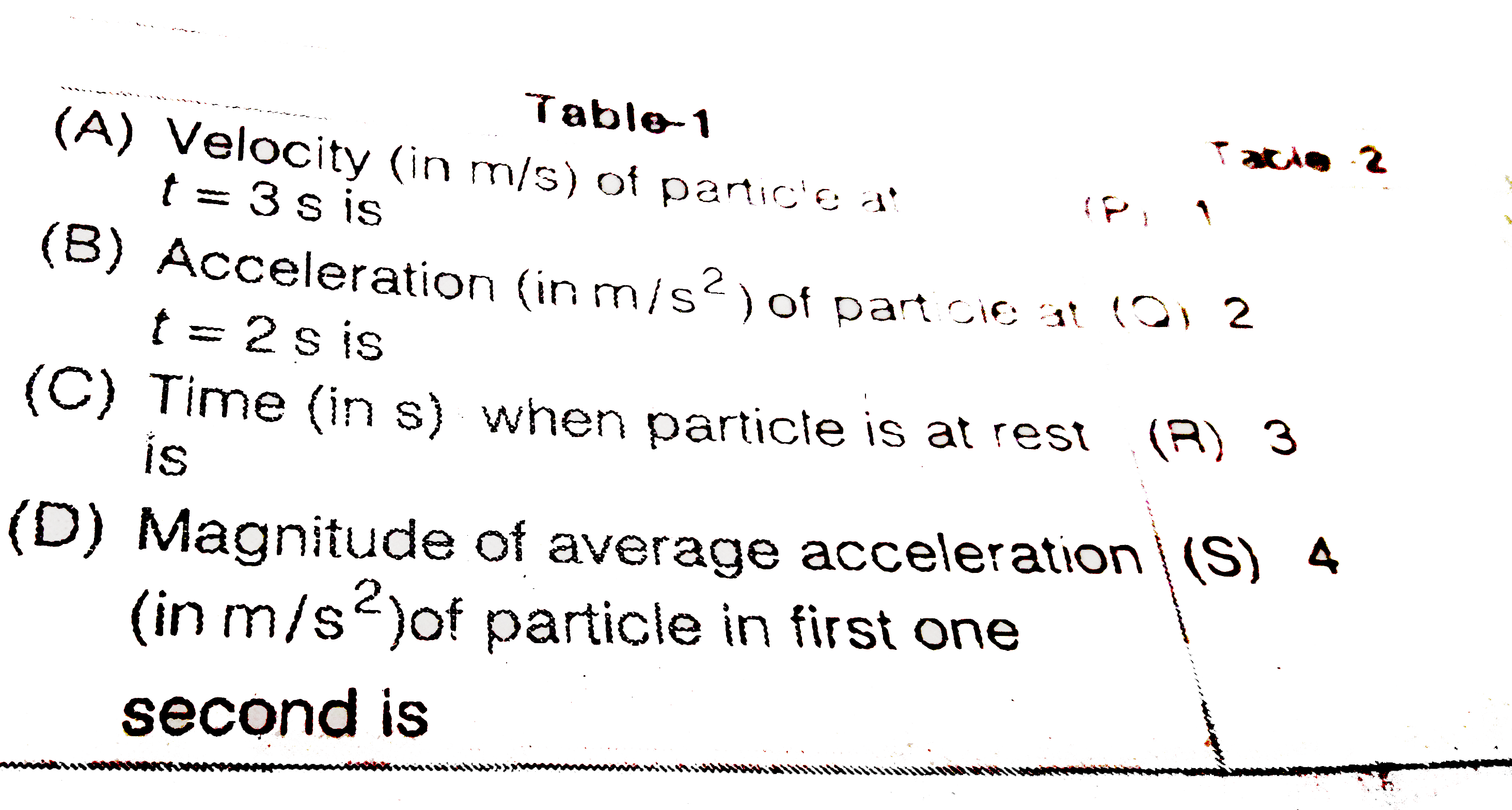
View SolutionThe relation between time t and displacement x is t=αx2+βx, where αandβ are constants. The retardation is
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View SolutionThe magnitude of radius vector of a point varies with time as r=βt(1−αt) where α and β are positive constant. The distance travelled by this body over a closed path must be
View Solution
