Quantity I: Area of quadralateral DFDE, given ABCD is a reactangle haing AB= 10 cm & BC = 12 cm.
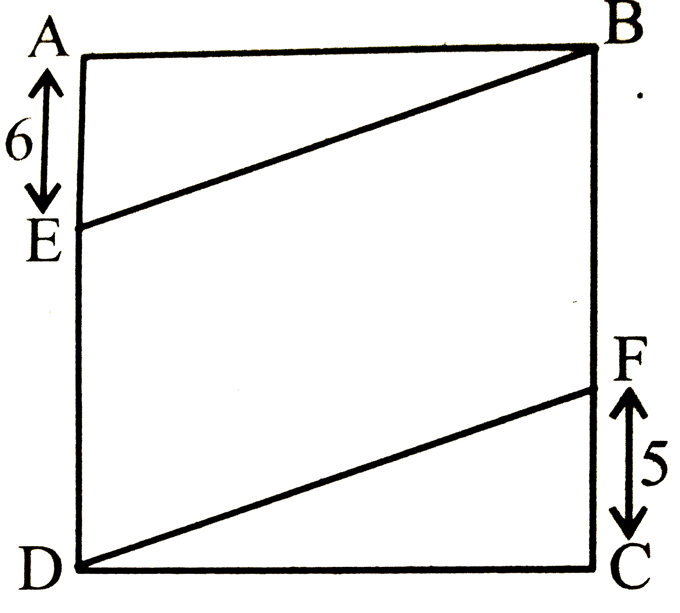
Quantity II: 15cm2
Quantity I > Quantity II
Quantity I < Quantity II
Quantity I ≥ Quantity II
Quantity I ≤ Quantity II
The correct Answer is:A
Area of quadrilateral BFDE = Area of rectangle ABCD - Area of ΔABEofΔDCF
=120−30−25=65
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a rectangle ABCD, AB= 15 cm ∠BAC=60∘ then BC is equal to
A15√3B15√32C15√3D152√3 - Question 2 - Select One
Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A220cm2B150cm2C120cm2D175cm2
Find the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View SolutionFind the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
View SolutionFind the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View SolutionFind the area of a quadrilateral ABCD is which AB=3cm, BC=4cm, CD=4cm, DA=5cm and AC=5cm
S=12(a+b+c)=12(3+4+5)=6
arof ABC=sqrt(s(s-a)(s-b)(s-c)<br>ar ABC=√6(6−3)(6−4)(6−5)
⇒√6×3×2×1=6cm2
Now in △ADC,S=a+b+c2
⇒s=5+4+52=142=7cm
By using Heron’s formula
Area of △ADC=√s(s−a)(s−b)(s−c)
=√7(7−5)(7−4)(7−5)
=√7×2×3×2
=2√21cm2
Area of△ADC=9.2cm2 (approx.)
Area of the quadrilateral ABCD = Area of △ADC+Areaof△ABC=9.2cm2+6cm2=15.2cm2
Thus, the area of the quadrilateral,ABCDis15.2cm2.View SolutionFind the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View Solution

